
分析 (1)根据关系式:C(x)=$\frac{k}{3x+8}$(0≤x≤10),无隔热层,则每年能源消耗费用为5万元,可求C(x),利用f(x)为隔热层建造费用与使用20年的能源消耗费用之和,可求函数关系式;
(2)利用基本不等式,即可求得函数的最小值.
解答 解:(1)当x=0时,C=5,因为C(x)=$\frac{k}{3x+8}$(0≤x≤10),所以k=40,故C(x)=$\frac{40}{3x+8}$…(3分)
∵f(x)为隔热层建造费用与使用20年的能源消耗费用之和
∴f(x)=6x+20×$\frac{40}{3x+8}$(0≤x≤10).…(6分)
(2)f(x)=6x+20×$\frac{40}{3x+8}$=2(3x+8)+20×$\frac{40}{3x+8}$-16≥2$\sqrt{1600}$-16=64,…(9分)
当且仅当2(3x+8)=20×$\frac{40}{3x+8}$,
即x=4时取得最小值.…(11分)
即隔热层修建4厘米厚时,总费用达到最小值,最小值为64万元.…(12分)
点评 本题考查函数模型的构建,考查利用基本不等式求函数的最值,考查学生的阅读能力,建立函数模型是关键.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 推理形式错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
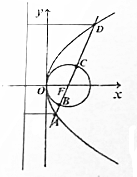 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com