
分析 (Ⅰ)求出f(x)的定义域,以及导函数,根据导函数的正负与增减性的关系判断即可确定出f(x)的单调区间;
(Ⅱ)令g(x)=ax+$\frac{a-1}{x}$-2a+1-lnx,x∈[1,+∞),求出g(1)的值以及导函数,根据导函数的正负与增减性的关系确定出f(x)≥lnx在[1,+∞)上恒成立时实数a的取值范围即可;
(Ⅲ)令a=$\frac{1}{2}$,根据第二问的结论列出关系式,进而可得当lnx2<x-$\frac{1}{x}$(x>1)(*),所证不等式等价于ln$\frac{2}{n(n+1)}$>$\frac{2-n-{n}^{2}}{\sqrt{2n(n+1)}}$,令x=$\sqrt{\frac{n(n+1)}{2}}$>1(n>2),代入不等式(*),整理即可得证.
解答 (Ⅰ)解:f(x)的定义域为{x|x≠0},f′(x)=a-$\frac{a-1}{{x}^{2}}$=$\frac{a{x}^{2}+1-a}{{x}^{2}}$(a>0),
当0<a≤1时,f'(x)>0恒成立,此时,f(x)在(-∞,0),(0,+∞)上是增函数;
当a≥1时,令f'(x)=0得:x1=-$\sqrt{\frac{a-1}{a}}$,x2=$\sqrt{\frac{a-1}{a}}$,
列表如下:
| x | (-∞,x1) | (x1,0) | (0,x2) | (x2,+∞) |
| f'(x) | + | _ | _ | + |
| f(x) | 增 | 减 | 减 | 增 |
点评 此题考查了利用导数求闭区间上函数的最值,以及利用导数研究函数的增减性,以及恒成立问题,熟练掌握导函数的性质与函数增减性的关系是解本题的关键.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:选择题
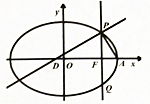 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com