
分析 分n为奇数、偶数两种情况讨论,利用分组求和法计算即得结论.
解答 解:当n为偶数时,Sn=[(-1+2)+(-3+4)+…+(-n+1+n)]+(2+22+…+2n)
=$\frac{n}{2}$+$\frac{2(1-{2}^{n})}{1-2}$
=2n+1+$\frac{n}{2}$-2;
当n为奇数时,Sn=[(-1+2)+(-3+4)+…+(-n+2+n-1)-n]+(2+22+…+2n)
=$\frac{n-1}{2}$-n+$\frac{2(1-{2}^{n})}{1-2}$
=2n+1-$\frac{n}{2}$-$\frac{5}{2}$;
综上所述,Sn=$\left\{\begin{array}{l}{{2}^{n+1}-\frac{n+5}{2},}&{n为奇数}\\{{2}^{n+1}+\frac{n-4}{2},}&{n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查分组求和法,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | 1 | C. | -1 | D. | ±$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
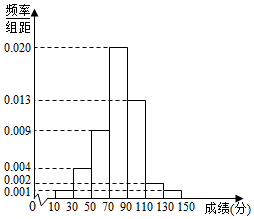 襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com