
分析 (I)由圆的切线的性质可得切线的方程,代入抛物线的方程,运用韦达定理和判别式大于0,结合中点坐标公式,解方程可得P的坐标;
(Ⅱ)假设存在实数k,使得以AB为底边的等腰△OAB恰有三个.即有P为AB的中点,且OP⊥AB,即l是圆的切线,且AB的中点为切点.联立切线的方程和抛物线的方程,运用判别式大于0,结合(I)的三个点,代入判别式,即可得到所求k的范围.
解答 解:(I)由题意可得m2+n2=2,
由切线的性质可得l的斜率为-$\frac{m}{n}$,
可得切线的方程为mx+ny=2,
设A(x1,y1),B(x2,y2),
联立曲线方程y=x2+x-2,可得nx2+(n+m)x-2n-2=0,
即有x1+x2=-$\frac{n+m}{n}$,
由点P恰好是线段AB的中点,可得-$\frac{n+m}{n}$=2m,
即有n+m+2mn=0,又m2+n2=2,
解得$\left\{\begin{array}{l}{m=-1}\\{n=-1}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{1-\sqrt{3}}{2}}\\{n=\frac{1+\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{1+\sqrt{3}}{2}}\\{n=\frac{1-\sqrt{3}}{2}}\end{array}\right.$.
代入△=(n+m)2+4n(2n+2)>0,可得
P的坐标为(-1,-1),或($\frac{1-\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$);
(Ⅱ)假设存在实数k,使得以AB为底边的等腰△OAB恰有三个.
即有P为AB的中点,且OP⊥AB,即l是圆的切线,且AB的中点为切点.
由$\left\{\begin{array}{l}{mx+ny=2}\\{y={x}^{2}+x+k}\end{array}\right.$,可得nx2+(n+m)x+kn-2=0,
同(I)解得$\left\{\begin{array}{l}{m=-1}\\{n=-1}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{1-\sqrt{3}}{2}}\\{n=\frac{1+\sqrt{3}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{1+\sqrt{3}}{2}}\\{n=\frac{1-\sqrt{3}}{2}}\end{array}\right.$.
满足△=(n+m)2-4n(kn-2)>0,即有k<$\frac{1+mn+4n}{2{n}^{2}}$,
代入点的坐标可得$\left\{\begin{array}{l}{k<-1}\\{k<-1+\frac{3\sqrt{3}}{2}}\\{k<-1-\frac{3\sqrt{3}}{2}}\end{array}\right.$,
即有k的范围是k<-1-$\frac{3\sqrt{3}}{2}$.
综上可得,存在k<-1-$\frac{3\sqrt{3}}{2}$,使得以AB为底边的等腰△OAB恰有三个.
点评 本题考查圆的切线与抛物线的位置关系,考查直线方程和抛物线的方程联立,运用韦达定理和判别式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
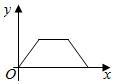 如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )
如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )| A. |  | B. |  | C. | 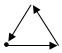 | D. | 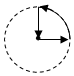 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.
如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 教材曾有介绍:圆x2+y2=r2上的点(x0,y0)处的切线方程为x${\;}_{0}x+{y}_{0}y={r}^{2}$,我们将其结论推广:椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点(x0,y0)处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}=1$,在解本题时可以直接应用,已知:直线x-y+$\sqrt{3}$=0与椭圆E:$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1(a>1)有且只有一个公共点;
教材曾有介绍:圆x2+y2=r2上的点(x0,y0)处的切线方程为x${\;}_{0}x+{y}_{0}y={r}^{2}$,我们将其结论推广:椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点(x0,y0)处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}=1$,在解本题时可以直接应用,已知:直线x-y+$\sqrt{3}$=0与椭圆E:$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1(a>1)有且只有一个公共点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com