解:∵E为BC的中点,且BC=6cm,
∴BE=EC=

BC=3cm,
又四边形ABCD为矩形,
∴AB=CD,∠B=∠C=90°,又BE=CE,
∴△ABE≌△DCE(SAS),
∴AE=DE,
∴∠EAD=∠EDA,
又△ABE为直角三角形,AB=4cm,BE=3cm,
根据勾股定理得:AE=5cm,
∴AE=DE=5cm,
∵AD∥BC,
∴∠AEB=∠EAD=∠EDA,
∴sin∠EAD=sin∠EDA=sin∠AEB=

=

,
当P在AE上时,0≤x≤

=

,
此时y=

AP•AD•sin∠PAD=

×2x×6×

=

x;
当P在ED上时,

≤x≤
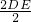
=5,
此时y=

AD•DP•sin∠ADP=

×6×(10-2x)×

=-

x+24;
当P在DA边上时,5<x≤8,S
△APO=0,
综上所述,x与y之间的函数关系为:
y=

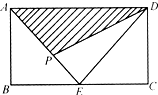
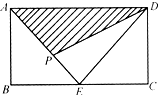
分析:由E为BC的中点,得到BE=CE,再根据ABCD为矩形,得到对边AB与CD相等,∠B和∠C都为直角,利用SAS可证明三角形ABE与三角形DCE全等,可得对应边AE与DE相等,根据等边对等角可得一对角相等,由两直线平行,内错角相等得到一对内错角相等,在三角形ABE中,利用锐角三角函数定义求出sin∠AEB的值,进而确定出sin∠EAD与sin∠EDA的值,利用分三种情况考虑:当P在AE上,P在DE上级P在AD上时,利用三角形的面积公式即可表示出y与x的函数关系式.
点评:此题属于根据实际问题选择函数类型的题,涉及的知识有:矩形的判定与性质,锐角三角函数定义,三角形的面积公式,利用了数形结合及分类讨论的数学思想,是一道综合性较强的题.

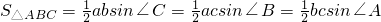
 BC=3cm,
BC=3cm,
 =
= ,
, =
= ,
, AP•AD•sin∠PAD=
AP•AD•sin∠PAD= ×2x×6×
×2x×6× =
= x;
x; ≤x≤
≤x≤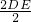 =5,
=5, AD•DP•sin∠ADP=
AD•DP•sin∠ADP= ×6×(10-2x)×
×6×(10-2x)× =-
=- x+24;
x+24;


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案