
分析 (1)设$φ(x)=g(x)-\frac{x}{2}=lnx-\frac{x}{2}$,求出φ(x)的导数,根据函数的单调性求出φ(x)的最大值小于0,从而证出结论;
(2)①得到h(x)=x2+ax-a2lnx,求出h(x)的导数,通过讨论a的范围求出h(x)的最小值,从而求出a的范围即可;
②问题胡宗南华为$b≥\frac{{{x^2}-2x}}{x-lnx}$在(0,+∞)上有解,设$F(x)=\frac{{{x^2}-2x}}{x-lnx}$,根据F(x)的单调性,求出F(x)的最小值,从而求出b的范围即可.
解答 解:(1)设$φ(x)=g(x)-\frac{x}{2}=lnx-\frac{x}{2}$,
则$φ'(x)=\frac{1}{x}-\frac{1}{2}=\frac{2-x}{2x}(x>0)$---(1分)
∴φ(x)在(0,2)上单调递增,在(2,+∞)上单调递减,--------(2分)
∴φ(x)max=φ(2)=ln2-1<0,
∴φ(x)<0,即$g(x)<\frac{x}{2}$---------------(3分)
(2)h(x)=x2+ax+blnx
①∵a2+b=0,∴h(x)=x2+ax-a2lnx
则$h'(x)=2x+a-\frac{a^2}{x}=\frac{{2{x^2}+ax-{a^2}}}{x}=\frac{(2x-a)(x+a)}{x}(x>0)$---------(4分)
(ⅰ)当a=0时,h(x)=x2>0恒成立;------------(5分)
(ⅱ)当a>0时,h(x)在$(0,\frac{a}{2})$上单调递减,在$(\frac{a}{2},+∞)$上单调递增,
∴$h{(x)_{min}}=h(\frac{a}{2})=\frac{3}{4}{a^2}-{a^2}ln\frac{a}{2}>0$,解得$0<a<2{e^{\frac{3}{4}}}$---------------(6分)
(ⅲ)当a<0时,h(x)在(0,-a)上单调递减,在(-a,+∞)上单调递增,
∴$h{(x)_{min}}=h(-a)=-{a^2}ln(-a)>0$,解得-1<a<0--------------(7分)
综上所述,a的取值范围为$-1<a<2{e^{\frac{3}{4}}}$---------------------(8分)
②∵h(x)在(0,+∞)上存在零点,
∴x2+ax+blnx=0在(0,+∞)上有解,
即$a=-x-\frac{blnx}{x}$在(0,+∞)上有解,
∵a+b≥-2,∴$-x-\frac{blnx}{x}+b≥-2$在(0,+∞)上有解,
由(1)可得$lnx<\frac{x}{2}<x$,
∴$b≥\frac{{{x^2}-2x}}{x-lnx}$在(0,+∞)上有解,
设$F(x)=\frac{{{x^2}-2x}}{x-lnx}$,则$F'(x)=\frac{(x-1)(x-2lnx+2)}{{{{(x-lnx)}^2}}}$,
∵$lnx<\frac{x}{2}$,∴x-2lnx+2>0,
∴F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴F(x)min=F(1)=-1,
故b≥-1----------------------------------(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.


科目:高中数学 来源: 题型:选择题
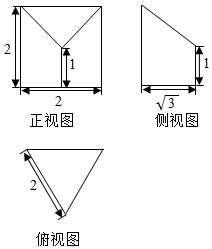 如图是某几何体的三视图,则该几何体体积是( )
如图是某几何体的三视图,则该几何体体积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 1或7 | D. | -1或-7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com