
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
分析 由正弦函数的对称轴,可得x0=km+$\frac{1}{2}$m,f(x0)=±$\sqrt{3}$,代入不等式,化为m2(k+$\frac{3}{2}$)($\frac{1}{2}$-k)>3,求得k的范围,取整数k=-1,0,代入不等式,解不等式可得m的范围.
解答 解:由函数f(x)=$\sqrt{3}$sin$\frac{πx}{m}$,函数f(x)的对称轴为x=x0,
可得$\frac{π{x}_{0}}{m}$=kπ+$\frac{π}{2}$,k∈Z,
即有x0=km+$\frac{1}{2}$m,f(x0)=±$\sqrt{3}$,
则存在x0满足${x}_{0}^{2}$+[f(x0)]2<m2,
即为(km+$\frac{1}{2}$m)2+3<m2,
化为m2(k+$\frac{3}{2}$)($\frac{1}{2}$-k)>3,
由(k+$\frac{3}{2}$)($\frac{1}{2}$-k)>0,可得
-$\frac{3}{2}$<k<$\frac{1}{2}$,即有整数k=-1,0,
当k=-1,0时,$\frac{3}{4}$m2>3,
解得m>2或m<-2.
故选:C.
点评 本题考查存在性问题的解法,考查正弦函数的对称性和最值,同时考查二次不等式的解法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
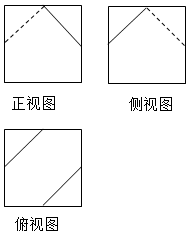 一个棱长为4的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( )
一个棱长为4的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为( )| A. | 40 | B. | $\frac{136}{3}$ | C. | 56 | D. | $\frac{184}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
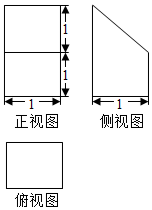 某几何体的三视图如图所示,则该几何体的表面积等于( )
某几何体的三视图如图所示,则该几何体的表面积等于( )| A. | 7+$\sqrt{2}$ | B. | 6+$\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,小华单位的圆柱形注水罐的底面半径为2m、高为3m,若每小时灌入该注水罐的水的体积为3m3,则经过多少小时该注水罐灌满?(注意:π取近似值3)
如图所示,小华单位的圆柱形注水罐的底面半径为2m、高为3m,若每小时灌入该注水罐的水的体积为3m3,则经过多少小时该注水罐灌满?(注意:π取近似值3)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 广告费用x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com