Question

18．已知二次函数的图象关于直线x=$\frac{3}{2}$对称，其与x轴两交点间距离为1，由顶点与两交点构成三角形的面积为$\frac{1}{8}$，求二次函数的解析式．

Answer 1

分析 画出函数的图象，求出抛物线的顶点坐标，设出二次函数的顶点式方程，将点（1，0）代入，求出抛物线的解析式即可．

解答 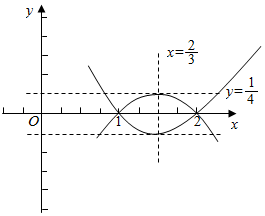解：如图示：，
函数的对称轴是x=$\frac{3}{2}$，函数与x轴两交点间距离为1，
故交点坐标是（1，0），（2，0），
又由顶点与两交点构成三角形的面积为$\frac{1}{8}$，
设三角形的高是h，
∴$\frac{1}{2}$×1×h=$\frac{1}{8}$，解得：h=$\frac{1}{4}$，
故抛物线的顶点坐标是（$\frac{3}{2}$，$\frac{1}{4}$）或（$\frac{3}{2}$，-$\frac{1}{4}$），
设抛物线方程是：y=a（x-$\frac{3}{2}$）²±$\frac{1}{4}$，
将（1，0）代入方程，解得：a=±1，
∴二次函数的解析式是：y=${（x-\frac{3}{2}）}^{2}$-$\frac{1}{4}$或y=-${（x-\frac{3}{2}）}^{2}$+$\frac{1}{4}$．

点评 本题考查了二次函数的性质，考查求函数的解析式问题，是一道中档题．．