
分析 根据题意,利用等差数列的前n项和公式,结合一元二次不等式的解法与步骤,利用判别式列出不等式,求出解集即可.
解答 解:等差数列{an}是有穷数列,且a1∈R,公差d=2,记{an}的所有项之和为S,
∴Sn=na1+$\frac{1}{2}$n(n-1)d=na1+n(n-1);
又a12+S≤96,
∴${{a}_{1}}^{2}$+na1+n(n-1)≤96,
即${{a}_{1}}^{2}$+na1+(n2-n-96)≤0;
∴△=n2-4(n2-n-96)≥0,
即3n2-4n-384≤0,
解得-$\frac{32}{3}$≤n≤12;
∴数列{an}至多有12项.
故答案为:12.
点评 本题考查了一元二次不等式的应用问题,也考查了等差数列的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
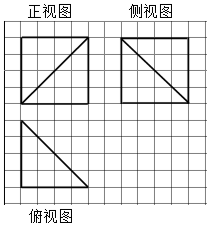 如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )| A. | $\frac{32}{3}$ | B. | 16 | C. | $\frac{64}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )
如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )| A. | 直角梯形、面积是16$\sqrt{2}$ | B. | 直角梯形、面积是8 | ||
| C. | 梯形非直角,面积是16 | D. | 梯形非直角,面积是8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com