
分析 运用分段函数的形式,求得f(x)的解析式,分别求得f(x)在两段上的最大值,注意运用二次函数的对称轴和区间的关系.
解答 解:∵a?b=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,
∴f(x)=(3x2+6x)?(2x+3-x2)=$\left\{\begin{array}{l}{3{x}^{2}+6x,-\frac{3}{2}≤x≤\frac{1}{2}}\\{2x+3-{x}^{2},x>\frac{1}{2}或x<-\frac{3}{2}}\end{array}\right.$,
当-$\frac{3}{2}$≤x≤$\frac{1}{2}$时,f(x)=3x2+6x=3(x+1)2-3,
可得f(x)在x=-1处取得最小值-3;在x=$\frac{1}{2}$处取得最大值$\frac{15}{4}$;
当x>$\frac{1}{2}$或x<-$\frac{3}{2}$时,f(x)=-x2+2x+3=-(x-1)2+4,
当x=1时,f(x)取得最大值4.
综上可得,f(x)的最大值为4.
故答案为:4.
点评 本题主要考查了函数的最值的求法,注意运用新定义,以及二次不等式的解法,考查二次函数在闭区间上的最值的求法,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:选择题
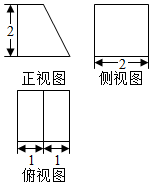
| A. | $\frac{20}{3}$cm3 | B. | $\frac{22}{3}$cm3 | C. | 4cm3 | D. | 6cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2lnx | B. | $\frac{1}{2}$lnx | C. | ln(2x) | D. | ln($\frac{1}{2}$x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com