
分析 (Ⅰ)f1(7)=$\underset{max}{{k}_{i}=0,1,2,3}${3xi}=max{0,3,6,9}=9;
(Ⅱ)f2(7)=$\underset{max}{{x}_{i}=0,1,2}${4x2+f1(7-3x2)}=max{0+f1(7),4+f1(4),8+f1(1)},即可求f2(7)的值,以及此时的x1,x2的值;
(Ⅲ)求得f3(11)的值时,得到x1=4,x2=0,x3=1,即可写出p的取值范围.
解答 解:(Ⅰ)f1(7)=$\underset{max}{{k}_{i}=0,1,2,3}${3xi}=max{0,3,6,9}=9,当x1=3时,f1(7)=9;
(Ⅱ)f2(7)=$\underset{max}{{x}_{i}=0,1,2}${4x2+f1(7-3x2)}=max{0+f1(7),4+f1(4),8+f1(1)},
x2=1时,f1(4)$\underset{max}{{x}_{i}=0,1,2}${3xi}=max{0,3,6}=6,∴x1=2时,f1(4)=6,
x2=2时,f1(1)=$\underset{max}{{x}_{i}=0}\{2{x}_{i}\}$=0,∴x1=0时,f1(1)=0,
∴f2(7)=max{9,4+6,8+0}=10,即x2=1,x1=2时,f2(7)=10;
(Ⅲ)求得f3(11)的值时,得到x1=4,x2=0,x3=1,4<p≤4.5.
点评 本题考查进行简单的合情推理,考查新定义,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
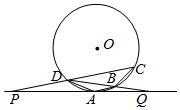 如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.
如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
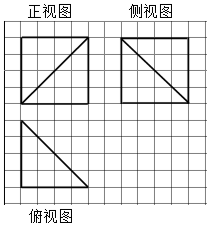 如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )| A. | $\frac{32}{3}$ | B. | 16 | C. | $\frac{64}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
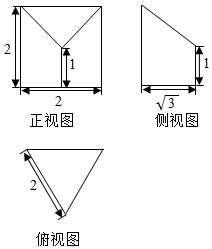 如图是某几何体的三视图,则该几何体体积是( )
如图是某几何体的三视图,则该几何体体积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com