练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．有一段演绎推理：“直线平行于平面，则这条直线平行于平面内所有直线；已知直线b?平面α，直线a?平面α，直线b∥平面α，则直线b∥直线a”的结论是错误的，这是因为（　　）
    A．大前提错误B．小前提错误C．推理形式错误D．非以上错误

    分析 分析该演绎推理的三段论，即可得出错误的原因是什么．

    解答 解：该演绎推理的大前提是：若直线平行于平面，则该直线平行于平面内所有直线；
    小前提是：已知直线b∥平面α，直线a?平面α；
    结论是：直线b∥直线a；
    该结论是错误的，因为大前提是错误的，
    正确叙述是“若直线平行于平面，过该直线作平面与已知平面相交，则交线与该直线平行”．
    故选：A．

    点评 本题通过演绎推理的三段论叙述，考查了空间中线面平行的性质定理的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．已知函数f（x）=$\left\{\begin{array}{l}x+1，x≤0\\{log_2}x，x＞0\end{array}$，则函数y=f（f（x））+1的所有零点构成的集合为$\left\{{-3，-\frac{1}{2}，\frac{1}{4}，\sqrt{2}}\right\}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知抛物线C：y2=4x的焦点为F，过点F且倾斜角为$\frac{π}{3}$的直线与抛物线C相交于P，Q两点，则弦PQ的长为（　　）
    A．3B．4C．5D．$\frac{16}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

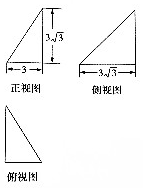    16．已知某几何体的三视图如图所示，则该几何体的内切球的体积为（　　）
    A．$\frac{1}{4}$πB．$\frac{\sqrt{3}}{4}$πC．$\frac{1}{2}$πD．$\frac{\sqrt{3}}{2}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

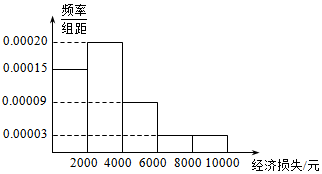    3．据四川省民政厅报告，2013年6月29日以来，四川省中东部出现强降雨天气过程，局地出现大暴雨．暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县（市、区）244万人受灾，共造成直接经济损失85502.41万元．适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．
    （1）小王向班级同学发出为该小区居民捐款的倡议．现请你解决下列两个问题：
    ①若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
    ②若从损失超过4000元的居民中随机抽出2户进行捐款援助，设抽出损失超过8000元的居民为ξ户，求ξ的分布列和数学期望．
    （2）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
    经济损失不超过4000元经济损失超过4000元合计
    捐款超过500元30939          
    捐款不超过500元5611
    合计351550
    351550
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    附：临界值表参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知O为△ABC的外心，AB=2，AC=3，如果$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$，其中x、y满足x+2y=1且xy≠0，则cos∠BAC=$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为$\frac{π}{3}$，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$2\sqrt{3}$，|$\overrightarrow{a}$+$\overrightarrow{b}$|•|$\overrightarrow{a}$-$\overrightarrow{b}$|的值是$\sqrt{21}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设函数y=f（x）是定义域为R，并且满足f（x+y）=f（x）+f（y），f（$\frac{1}{3}$）=1，且x＞0时，f（x）＞0
    （1）求f（0）值
    （2）判断函数奇偶性并证明
    （3）如果f（x）+f（2+x）＜2，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知复数z满足$iz=\frac{4+3i}{1+2i}$，则复数z在复平面内对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案