
分析 由(2$\overrightarrow{a}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$)得(2$\overrightarrow{a}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,展开后代入数量积公式,结合|$\overrightarrow{a}$|=$|λ\overrightarrow{b}|$可求实数λ的值.
解答 解:由(2$\overrightarrow{a}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$),得(2$\overrightarrow{a}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
∴$2|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}=0$,
∵非零向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,且|$\overrightarrow{a}$|=$|λ\overrightarrow{b}|$,
∴$2{λ}^{2}|\overrightarrow{b}{|}^{2}+2|λ|•|\overrightarrow{b}|•|\overrightarrow{b}|cos\frac{2π}{3}=0$,
即2λ2-|λ|=0,
由题意知λ≠0,∴|λ|=$\frac{1}{2}$,得$λ=±\frac{1}{2}$.
故答案为:$±\frac{1}{2}$.
点评 本题考查平面向量的数量积运算,关键是熟记数量积公式,是基础题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{3}$,0]上是增函数 | B. | 在区间[0,$\frac{π}{3}$]上是减函数 | ||
| C. | 在区间[-$\frac{π}{6}$,0]上是减函数 | D. | 在区间[-$\frac{π}{6}$,$\frac{π}{6}$]上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
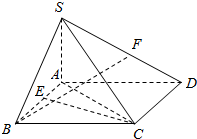 如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.
如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com