
分析 (1)利用两角和的余弦及倍角公式化简,求出函数的最大值,再由周期公式求周期;
(2)由f($\frac{C}{2}$)=-$\frac{1}{4}$,得sinC=$\frac{\sqrt{3}}{2}$,进一步得到cosC=$\frac{1}{2}$.又cosB=$\frac{1}{3}$,得sinB=$\frac{2\sqrt{2}}{3}$,求出sinA,然后利用正弦定理求得BC的长度.
解答 解:(1)f(x)=cos(2x+$\frac{π}{3}$)+sin2x=$cos2xcos\frac{π}{3}-sin2xsin\frac{π}{3}+si{n}^{2}x$
=$\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x+\frac{1-cos2x}{2}$=$-\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}$.
∴函数f(x)的最大值为$\frac{\sqrt{3}+1}{2}$.
最小正周期$T=\frac{2π}{2}=π$;
(2)由f($\frac{C}{2}$)=-$\frac{1}{4}$,得$-\frac{\sqrt{3}}{2}sinC+\frac{1}{2}=-\frac{1}{4}$,∴sinC=$\frac{\sqrt{3}}{2}$,
∵C为锐角,∴C=60°,cosC=$\frac{1}{2}$.
又cosB=$\frac{1}{3}$,∴sinB=$\frac{2\sqrt{2}}{3}$,
则sinA=sin(B+C)=sinBcosC+cosBsinC=$\frac{2\sqrt{2}}{3}×\frac{1}{2}+\frac{1}{3}×\frac{\sqrt{3}}{2}=\frac{2\sqrt{2}+\sqrt{3}}{6}$.
由正弦定理得:$\frac{AC}{sinB}=\frac{BC}{sinA}$,即$\frac{2\sqrt{2}}{\frac{2\sqrt{2}}{3}}=\frac{BC}{\frac{2\sqrt{2}+\sqrt{3}}{6}}$,
∴$BC=\sqrt{2}+\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数中的恒等变换应用,考查了三角函数的性质,训练了正弦定理在解三角形中的应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
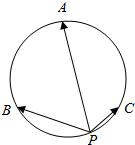 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )| A. | (-1):2:3 | B. | (-3):2:1 | C. | (-2):3:6 | D. | (-6):3:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com