
| x | 2 | 3 | 4 | 5 | 6 |
| y | 3 | 4 | 6 | 8 | 9 |
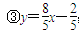 ;
;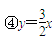 ,则根据最小二乘法的思想得拟合程度最好的直线是____________(填序号).
,则根据最小二乘法的思想得拟合程度最好的直线是____________(填序号). 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:不详 题型:单选题
| | 男 | 女 | 总计 |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.500人 | B.1000人 | C.1500人 | D.2000人 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
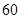 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
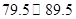 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少? 分及以上为及格)
分及以上为及格)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
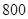 名男生中随机抽取
名男生中随机抽取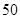 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于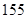 cm和
cm和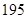 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[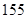 ,
,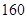 ),第二组[
),第二组[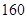 ,
,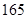 ),…,第八组[
),…,第八组[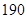 ,
,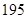 ],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为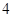 人.
人.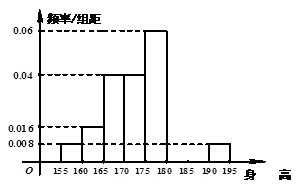
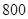 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在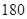 cm以上(含
cm以上(含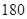 cm)的人数;
cm)的人数;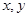 ,事件
,事件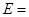 {
{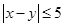 },事件
},事件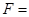 {
{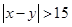 },求
},求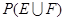 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
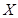 ,求
,求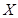 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.① | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com