
分析 由等差数列{an}的首项为1,公差为3,求出Sn=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$,再由Sn=35,得${S}_{n}=\frac{3}{2}{n}^{2}-\frac{1}{2}n=35$,由此能求出结果.
解答 解:∵等差数列{an}的首项为1,公差为3,
∴${S}_{n}=n{a}_{1}+\frac{n(n-1)}{2}d$=n+$\frac{n(n-1)}{2}×3$=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$,
∵Sn=35,∴${S}_{n}=\frac{3}{2}{n}^{2}-\frac{1}{2}n=35$,
解得n=5或n=-$\frac{14}{3}$(舍).
故答案为:5.
点评 本题考查等差数列的前n项和为35的项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,π) | B. | $[{\frac{π}{2},\frac{3π}{2}}]$ | C. | $[{-\frac{π}{2},\frac{π}{2}}]$ | D. | (π,2π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,-2) | C. | (-2,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
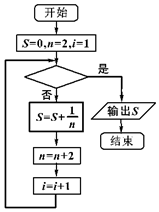 如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )| A. | i<11 | B. | i>11 | C. | i<22 | D. | i>22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com