
【题目】已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点, ![]() PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
A. (![]() ,+
,+![]() ) B. (
) B. (![]() ,+
,+![]() ) C. (
) C. (![]() ,+
,+![]() ) D. (0,+
) D. (0,+![]() )
)
科目:高中数学 来源: 题型:
【题目】若f(x)=ex+ae﹣x为偶函数,则f(x﹣1)< ![]() 的解集为( )
的解集为( )
A.(2,+∞)
B.(0,2)
C.(﹣∞,2)
D.(﹣∞,0)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|)。
(1)求实数a,b的值;
(2)若不等式f(2k)>1成立,求实数k的取值范围;
(3)定义在[p,q]上的函数![]() (x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
(x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() (x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
(x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点,F为AC和BD的交点.
(1)证明:PB∥平面AEC;
(2)证明:平面PAC⊥平面PBD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D. 
(1)证明:直线AB与⊙O相切;
(2)若∠CED的正切值为 ![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF. 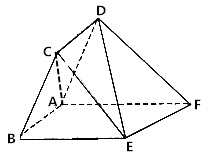
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com