
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①在区间(0,+∞)上,y=$\sqrt{x}$,y=x3是增函数;
②若logm3<logn3<0,则$\frac{1}{{log}_{3}^{m}}<\frac{1}{{log}_{3}^{n}}<0$⇒$0{>log}_{3}^{m}{>log}_{3}^{n}$则⇒0<n<m<1;
③奇函数关于原点对称,函数f(x)向右平移1个单位后,f(x-1)的图象关于点(1,0)对称;
④方程f(x)=0有两个实数根,就是函数f(x)=3x与f(x)=2x+3的交点.
解答 解:对于①在区间(0,+∞)上,y=$\sqrt{x}$,y=x3是增函数,故①错;
对于②若logm3<logn3<0,则$\frac{1}{{log}_{3}^{m}}<\frac{1}{{log}_{3}^{n}}<0$⇒$0{>log}_{3}^{m}{>log}_{3}^{n}$则⇒0<n<m<1,故②正确;
对于③奇函数关于原点对称,函数f(x)向右平移1个单位后,f(x-1)的图象关于点(1,0)对称,故③正确;
对于④方程f(x)=0有两个实数根,就是函数f(x)=3x与f(x)=2x+3的交点,画出图象即可看出交点是两个,故④正确.
故选:C
点评 本题考查了初等函数的基本性质及图象的变换,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log0.34<log0.36 | B. | 1.72.4>1.72.5 | C. | 2.50.2<2.40.2 | D. | log34>log43 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
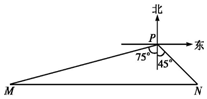 如图,一艘船自西向东匀速航行,上午10时到一座灯塔P的南偏西75°距塔68海里的M处,下午2时达这座灯塔的东南方向的N处,则这艘船航行的速度为( )
如图,一艘船自西向东匀速航行,上午10时到一座灯塔P的南偏西75°距塔68海里的M处,下午2时达这座灯塔的东南方向的N处,则这艘船航行的速度为( )| A. | $\frac{17\sqrt{6}}{2}$ 海里/时 | B. | 34$\sqrt{6}$海里/时 | C. | $\frac{17\sqrt{2}}{2}$海里/时 | D. | 34$\sqrt{2}$海里/时 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示是正方体的平面展开图,在这个正方体中( )
如图所示是正方体的平面展开图,在这个正方体中( )| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
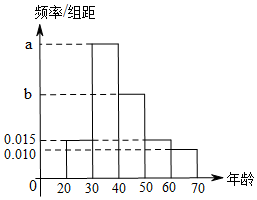 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com