
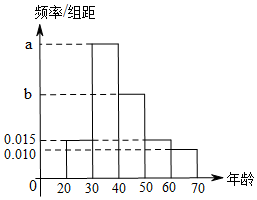
 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.分析 (1)由于五个组的频率之和等于1,故:0.015×10+10a+10b+0.015×10+0.01×10=1,且a-b=b-0.015,联立解出即可得出.
(2)由已知高消费人群所占比例为10(a+b)=0.6,潜在消费人群的比例为0.4.由分层抽样的性质知抽出的10人中,高消费人群有6人,潜在消费人群有4人.随机抽取的三人中代金券总和X可能的取值为:240,210,180,150.再利用“超几分布列”的概率计算公式及其数学期望即可得出.
解答 解:(1)由于五个组的频率之和等于1,故:0.015×10+10a+10b+0.015×10+0.01×10=1,且a-b=b-0.015
联立解出a=0.035,b=0.025
(2)由已知高消费人群所占比例为10(a+b)=0.6,潜在消费人群的比例为0.4,
由分层抽样的性质知抽出的10人中,高消费人群有6人,潜在消费人群有4人,
随机抽取的三人中代金券总和X可能的取值为:240,210,180,150.
$P(X=240)=\frac{C_4^3}{{C_{10}^3}}=\frac{1}{30}$;$P(X=210)=\frac{C_4^2C_6^1}{{C_{10}^3}}=\frac{3}{10}$$P(X=180)=\frac{C_4^1C_6^2}{{C_{10}^3}}=\frac{1}{2}$;$P(X=150)=\frac{C_6^3}{{C_{10}^3}}=\frac{1}{6}$
列表如下:
| X | 240 | 210 | 180 | 150 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
点评 本题考查了频率分布直方图“超几分布列”的概率计算公式及其数学期望、分层抽样的性质,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ③④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com