
分析 (1)由已知及正弦定理可得${a^2}+{b^2}-{c^2}=\frac{{\sqrt{10}}}{5}ab$,利用余弦定理可求cosC,利用同角三角函数基本关系式可求sinC,sinA的值,进而利用三角形内角和定理,诱导公式,两角和的余弦函数公式可求cosB,解得B的范围即可得解B的值.
(2)利用正弦定理可求c,进而利用三角形面积公式即可计算得解.
解答 解:(1)由已知可得${a^2}+{b^2}-{c^2}=\frac{{\sqrt{10}}}{5}ab$,
∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{{\sqrt{10}}}{10}$.
∵A,C∈(0,π),
∴$sinC=\frac{{3\sqrt{10}}}{10}$,$sinA=\frac{{2\sqrt{5}}}{5}$,
∴cosB=-cos(A+C)=-($\frac{\sqrt{5}}{5}×\frac{\sqrt{10}}{10}$-$\frac{3\sqrt{10}}{10}×\frac{2\sqrt{5}}{5}$)=$\frac{\sqrt{2}}{2}$,
∵B∈(0,π),
∴B=$\frac{π}{4}$.
(2)∵$\frac{b}{sinB}=\frac{c}{sinC}$=10$\sqrt{2}$,
∴c=10$\sqrt{2}×$$\frac{3\sqrt{10}}{10}$=6$\sqrt{5}$,
∴$S=\frac{1}{2}bcsinA=\frac{1}{2}×10×6\sqrt{5}×\frac{{2\sqrt{5}}}{5}=60$.
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式,三角形内角和定理,诱导公式,两角和的余弦函数公式,三角形面积公式在解三角形中的应用,考查了转化思想,熟练掌握相关公式的应用是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
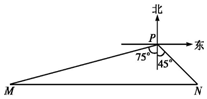 如图,一艘船自西向东匀速航行,上午10时到一座灯塔P的南偏西75°距塔68海里的M处,下午2时达这座灯塔的东南方向的N处,则这艘船航行的速度为( )
如图,一艘船自西向东匀速航行,上午10时到一座灯塔P的南偏西75°距塔68海里的M处,下午2时达这座灯塔的东南方向的N处,则这艘船航行的速度为( )| A. | $\frac{17\sqrt{6}}{2}$ 海里/时 | B. | 34$\sqrt{6}$海里/时 | C. | $\frac{17\sqrt{2}}{2}$海里/时 | D. | 34$\sqrt{2}$海里/时 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
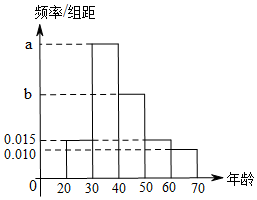 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
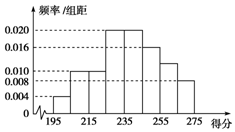 某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275).如图是按上述分组方法得到的频率分布直方图.
某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275).如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{4}$] | C. | (-∞,0)∪($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com