
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{4}$] | C. | (-∞,0)∪($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
分析 依题意,将“存在x1,x2∈[1,2],使$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0为假命题”转化为“?x1,x2∈[1,2],f′(x)=2ax-1≥0恒成立”,即可求得实数a的取值范围.
解答 解:存在x1,x2∈[1,2],使$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0为假命题
??x1,x2∈[1,2],使$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$≥0恒成立
??x1,x2∈[1,2],f′(x)=2ax-1≥0恒成立
?a≥${(\frac{1}{2x})}_{max}$=$\frac{1}{2}$.
即实数a的取值范围为:[$\frac{1}{2}$,+∞).
故选:D.
点评 本题考查命题的真假判断与应用,将“存在x1,x2∈[1,2],使$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0为假命题”转化为“?x1,x2∈[1,2],f′(x)=2ax-1≥0恒成立”是关键,也是难点,考查等价转化思想与导数的运用,属于难题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
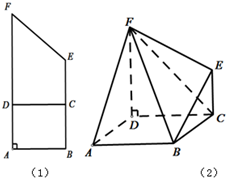 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=(0,+∞) | B. | (∁RA)∪B=(-∞,0] | C. | (∁RA)∩B={-2,-1} | D. | A∩(∁RB)=[0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com