
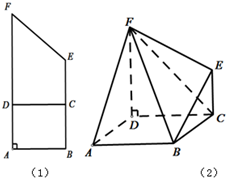
 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)分析 (1)以点D为坐标原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出异面直线BD与EF所成角的大小.
(2)连结AE,取中点为G,连结GA,GB,GC,GD,GE,得到DG长为所求球的半径,由此能求出过A、B、C、D、E这五个点的球的表面积.
解答 解:(1)以点D为坐标原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系,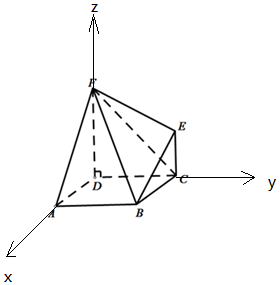
D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),E(0,1,1),F(0,0,2)
$\overrightarrow{DB}$=(1,1,0),$\overrightarrow{EF}$=(0,-1,1),
设异面直线BD与EF所成角为θ,
则cosθ=$\frac{|\overrightarrow{DB}•\overrightarrow{EF}|}{|\overrightarrow{DB}|•|\overrightarrow{EF}|}$=$\frac{1}{2}$,
∴$θ=\frac{π}{3}$,
∴异面直线BD与EF所成角的大小为$\frac{π}{3}$.
(2)连结AE,取中点为G,连结GA,GB,GC,GD,GE,
由已知得GA=GB=GC=GD=GE,
所以DG长为所求球的半径,
G($\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),$\overrightarrow{DG}$=($\frac{1}{2},\frac{1}{2},\frac{1}{2}$),
∴r=|$\overrightarrow{DG}$|=$\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$.
∴过A、B、C、D、E这五个点的球的表面积:
S=$4π{r}^{2}=4π×(\frac{\sqrt{3}}{2})^{2}$=3π.
点评 本题考查异面直线所成角的大小的求法,考查球的表面积的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{4}$] | C. | (-∞,0)∪($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{a}$,0) | B. | ($\frac{1}{2a}$,0) | ||
| C. | ($\frac{1}{4a}$,0) | D. | a>0 时为($\frac{1}{4a}$,0),a<0 时为(-$\frac{1}{4a}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
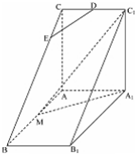 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,N是BC的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上的一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,N是BC的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 极大值为6,极大值为-26 | B. | 极大值为5,极大值为-26 | ||
| C. | 极大值为6,极大值为-25 | D. | 极大值为5,极大值为-25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1) | C. | (2)(3) | D. | (1)(2)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com