
分析 (1)由S1+$\frac{1}{16}$,S2,S3成等差数列,可得$2{S}_{2}={S}_{1}+\frac{1}{16}+{S}_{3}$,化简为${a}_{2}={a}_{3}+\frac{1}{16}$,又因为${a}_{2}=\frac{1}{8}$,解得a1和q,即可求出等比数列{an}的通项公式;
(2)因为{an}是等比数列,{bn}是等差数列,而cn=anbn,故利用错位相减法即可求出Tn=c1+c2+…+cn,将Tn和Sn代入不等式,并整理得$\frac{1}{2}λ≤2-\frac{n+1}{{2}^{n}}$,记f(n)=$\frac{n+1}{{2}^{n}}$,
利用作差法可得f(n)关于n单调递减,则f(n)max=f(1)=1,故$\frac{1}{2}λ≤2-1=1$,即λ≤2.
解答 解:(1)设数列{an}的公比为q,
∵${S_1}+\frac{1}{16},{S_2},{S_3}$成等差数列,∴$2{S_2}={S_1}+\frac{1}{16}+{S_3}$,∴${a_2}={a_3}+\frac{1}{16}$,
∵${a_2}=\frac{1}{8}$,∴${a_3}=\frac{1}{16}$,∴$q=\frac{a_3}{a_2}=\frac{1}{2}$,
∴${a_n}={a_2}{q^{n-2}}=\frac{1}{8}•{(\frac{1}{2})^{n-2}}={(\frac{1}{2})^{n+1}}$.
(2)设数列{cn}的前项n和为Tn,则Tn=c1+c2+c3+…+cn,
又${c_n}={a_n}{b_n}=2n•{(\frac{1}{2})^{n+1}}=\frac{n}{2^n}$,
∴${T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}$,$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{n}{{{2^{n+1}}}}$,
两式相减得$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}=\frac{{\frac{1}{2}(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n+1}}}}=1-\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}=1-\frac{n+2}{{{2^{n+1}}}}$,
∴${T_n}=2-\frac{n+2}{2^n}$,
又${S_n}=\frac{{\frac{1}{4}(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}=\frac{1}{2}(1-\frac{1}{2^n})$,
∴对任意n∈N+,不等式${c_1}+{c_2}+…+{c_n}≥\frac{1}{2}λ+2{S_n}-1$恒成立等价于${T_n}≥\frac{1}{2}λ+2{S_n}-1$恒成立,
即$2-\frac{n+2}{2^n}≥\frac{1}{2}λ+1-\frac{1}{2^n}-1$恒成立,即$2-\frac{n+1}{2^n}≥\frac{1}{2}λ$恒成立,
令$f(n)=\frac{n+1}{2^n}$,$f(n+1)-f(n)=\frac{n+2}{{{2^{n+1}}}}-\frac{n+1}{2^n}=\frac{-n}{{{2^{n+1}}}}<0$,
∴f(n)关于n单调递减,∴$2-\frac{2}{2}≥\frac{1}{2}λ$,∴λ≤2,
∴λ的取值范围为(-∞,2].
点评 本题考查了等差数列与等比数列的通项公式、错位相减求和及利用数列的单调性求最值,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
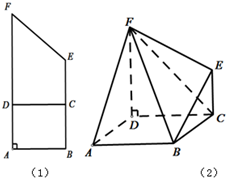 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-3,1) | C. | (1,+∞) | D. | (-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com