
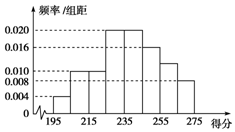
 ij��У��֯�����������ԣ�����2 000��ѧ�������μ��˱��ԣ��ɼ�������195�ֵ�275��֮�䣬���������ȡ50��ͬѧ�ijɼ�����ͳ�ƣ���ͳ�ƽ�������·�ʽ�ֳɰ��飺��һ��[195��205�����ڶ���[205��215���������ڰ���[265��275������ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��
ij��У��֯�����������ԣ�����2 000��ѧ�������μ��˱��ԣ��ɼ�������195�ֵ�275��֮�䣬���������ȡ50��ͬѧ�ijɼ�����ͳ�ƣ���ͳ�ƽ�������·�ʽ�ֳɰ��飺��һ��[195��205�����ڶ���[205��215���������ڰ���[265��275������ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ���������255��265֮���Ƶ�ʣ��ɴ��ܳ�����2 000��ѧ���У���ȡ1�ˣ�����˵ķ�����255��265֮��ĸ��ʣ�
��2����Ƶ�ʷֲ�ֱ��ͼ�������������2 000��ѧ����ƽ��������
��3����Ƶ�ʷֲ�ֱ��ͼ�������������λ�����ɴ��ܳ��ƻ����ɼ�ȡ1 000��ѧ���������Ի��ڣ�Ӧ�������߶�Ϊ���ٷ֣�
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�÷�����255��265֮���Ƶ��Ϊ��
1-��0.004+0.010��2+0.020��2+0.0165+0.008����10=0.12��
�����2 000��ѧ���У���ȡ1�ˣ�����˵ķ�����255��265֮��ĸ���Լ��0.12��
��2����Ƶ�ʷֲ�ֱ��ͼ�����ʵã�
��2 000��ѧ����ƽ������Ϊ��
200��0.004��10+210��0.010��10+220��0.010��10+230��0.020��10+240��0.020��10+250��0.016��10+260��0.12+270��0.008��10=237.8��
��3���ӵ�һ�鵽�����飬Ƶ��Ϊ0.04+0.1+0.1+0.2=0.44����0.5-0.44=0.06��
��������[235��245���������±����ָ$\frac{0.006}{0.2-0.006}$=$\frac{3}{7}$��
����λ��Ϊ235+3=238��
��ƻ����ɼ�ȡ1 000��ѧ���������Ի��ڣ�Ӧ�������߶�Ϊ238�֣�
���� ���⿼����ʡ�ƽ��������λ������Ӧ�ã��ǻ����⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -4 | C�� | 4 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | $\frac{5}{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����p��q�Ǽ����� | B�� | ����p��q�������� | ||
| C�� | ����p�ģ��Vq���Ǽ����� | D�� | ����p�ģ��Vq���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com