
下列说法:
①“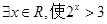 ”的否定是“
”的否定是“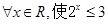 ”;
”;
②函数 的最小正周期是
的最小正周期是
③命题“函数 处有极值,则
处有极值,则 ”的否命题是真命题;
”的否命题是真命题;
④ 上的奇函数,
上的奇函数, 时的解析式是
时的解析式是 ,则
,则 时的解析式为
时的解析式为 其中正确的说法是 。
其中正确的说法是 。
科目:高中数学 来源: 题型:填空题
已知抛物线 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设 于
于 于
于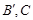 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ② ;
;
③ ; ④
; ④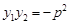 ; ⑤.
; ⑤. 
其中一定正确的有 (写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题中_________为真命题.
① “A∩B=A”成立的必要条件是“A B”,
B”,
②“若x2+y2=0,则x,y全为0”的否命题,
③“全等三角形是相似三角形”的逆命题,
④“圆内接四边形对角互补”的逆否命题。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列四个命题:
① 命题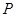 :
: ;则
;则 命题是;
命题是; ;
;
② (
(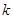 为正整数)的展开式中,
为正整数)的展开式中, 的系数小于90,则
的系数小于90,则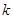 的值为1;
的值为1;
③从总体中抽取的样本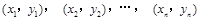 .若记
.若记 ,则回归直线
,则回归直线 必过点
必过点 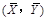 ;
;
④过双曲线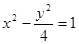 的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
其中正确的序号是 (把你认为正确的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com