
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 f(x)=e|x-a|=$\left\{\begin{array}{l}{{e}^{x-a},x≥a}\\{{e}^{a-x},x<a}\end{array}\right.$,利用指数函数与复合函数的单调性即可判断出结论.
解答 解:f(x)=e|x-a|=$\left\{\begin{array}{l}{{e}^{x-a},x≥a}\\{{e}^{a-x},x<a}\end{array}\right.$,
∴a≤1时,f(x)在区间[1,+∞)上为增函数.
∴“a=1”是“f(x)在区间[1,+∞)上为增函数”的充分不必要条件.
故选:A.
点评 本题考查了指数函数与复合函数的单调性、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
设函数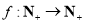 满足:对于任意大于3的正整数
满足:对于任意大于3的正整数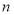 ,
,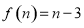 ,且当
,且当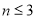 时,
时,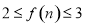 ,则不同的函数
,则不同的函数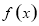 的个数为( )
的个数为( )
A.1 B.3 C.6 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{5π}{6}$ | B. | x=$\frac{7π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com