
分析 (Ⅰ)先画出约束条件$\left\{\begin{array}{l}{y≥0}\\{y≥x}\\{y≤2-x}\end{array}\right.$的可行域,再求出可行域中各角点的坐标,
(1)求出x+2y的最大值,然后求解z=3x+2y的最大值;
(2)利用|4x+3y+1|的几何意义,求解目标函数的最大值;
(3)利用(x+1)2+(y+1)2的几何意义求解最大值;
(4)z=$\frac{2y}{3x+9}$的几何意义求解表达式的最大值;
(5)化简z=$\frac{{x}^{2}-{y}^{2}}{xy}$的形式,通过直线的斜率求解表达式的最小值;
(6)化简z=x-y+|x+2y+3|的形式,利用几何意义求解最大值.
(Ⅱ)点(a+b,a-b)满足不等式,点的可行域,然后求2a+b的最大值.
解答 解:(Ⅰ)
(1)约束条件不等式组$\left\{\begin{array}{l}{y≥0}\\{y≥x}\\{y≤2-x}\end{array}\right.$的可行域如下图示: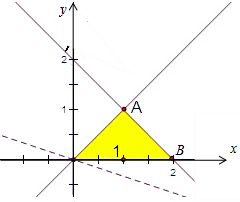
A(1,1);B(2,0),O(0,0)
由图易得目标函数z=3x+2y的最大值在A(1,1)处取得,z=3x+2y的最大值为:31+2=27.
(2)z=|4x+3y+1|的最大值,就是可行域内的点到直线4x+3y+1=0距离的5倍,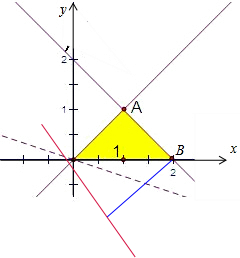
由图形可知B到直线4x+3y+1=0距离最大,
此时Z=|4x+3y+1|=9.
(3)z=(x+1)2+(y+1)2的几何意义是:可行域内的点与(-1,-1)距离的平方,易知B到(-1,-1)的距离最大,此时:Z=(2+1)2+(0+1)2=10.
(4)z=$\frac{2y}{3x+9}$=$\frac{2}{3}•\frac{y}{x+3}$的几何意义是可行域内的点与(-3,0)连线的斜率的$\frac{2}{3}$倍,
由图形可知,A与(-3,0)连线的斜率最大,可得:z=$\frac{2}{3+9}=\frac{1}{6}$;
(5)z=$\frac{{x}^{2}-{y}^{2}}{xy}$=$\frac{x}{y}$-$\frac{y}{x}$,$\frac{y}{x}$表示可行域的点与原点连线的斜率,$\frac{y}{x}$∈[0,1],-$\frac{y}{x}$∈[-1,0],$\frac{x}{y}$∈[1,+∞),
z=$\frac{{x}^{2}-{y}^{2}}{xy}$∈[0,+∞).z=$\frac{{x}^{2}-{y}^{2}}{xy}$的最小值的最小值为:0;
(6)z=x-y+|x+2y+3|=2x+y+3,平移直线2x+y+3=t,
当直线经过可行域的B点时,z取得最大值2×2+0+3=7.
(Ⅱ)点(a+b,a-b)满足不等式,可得:$\left\{\begin{array}{l}{0≤a+b≤2}\\{0≤a-b≤2}\end{array}\right.$,
不等式组:$\left\{\begin{array}{l}{0≤a+b≤2}\\{0≤a-b≤2}\end{array}\right.$,的可行域为: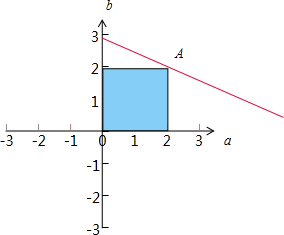
z=2a+b经过可行域的A点时,z取得最大值为:2×2+2=6.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.利用表达式的几何意义求解表达式的最值是解题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高一下学期期中数学试卷(解析版) 题型:解答题
在平面直角坐标系内,已知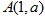 ,
, ,
,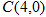 ;
;
(1)当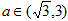 时,求直线
时,求直线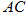 的倾斜角
的倾斜角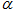 的取值范围;
的取值范围;
(2)当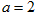 时,求
时,求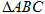 的
的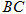 边上的高
边上的高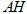 所在直线方程
所在直线方程 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com