
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
分析 根据有向线段的定义,向量的定义,以及向量的几何意义便可判断每个说法的正误,从而找出正确选项.
解答 解:①始点、方向、长度可以确定一条有向线段;
即有向线段三要素是始点、方向、长度,∴该说法正确;
②根据向量的定义知,向量的两要素是大小和方向,∴该说法正确;
③根据向量的定义知同向且等长的有向线段表示同一向量,∴该说法正确;
④∵$|\overrightarrow{AB}|=|\overrightarrow{DC}|$,且$\overrightarrow{AB}$与$\overrightarrow{DC}$方向相同,∴$\overrightarrow{AB}=\overrightarrow{DC}$;
∴该说法正确.
故选:D.
点评 考查有向线段、向量的定义,以及向量的几何意义,平行四边形的定义.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | (1,$\frac{\sqrt{3}}{2}$) | D. | (1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{5π}{6}$ | B. | x=$\frac{7π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
阅读如下程序框图,如果输出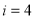 ,那么空白的判断框中应填入的条件是( )
,那么空白的判断框中应填入的条件是( )

A. B.
B.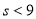 C.
C.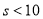 D.
D.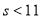
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com