
分析 (1)利用$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$即可得出.
(2)利用$\frac{1}{n(n+1)(n+2)}$=$\frac{1}{2}(\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)})$即可得出.
解答 解:(1)∵$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{8}-\frac{1}{10})$+$(\frac{1}{9}-\frac{1}{11})]$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{10}-\frac{1}{11})$
=$\frac{36}{55}$.
(2)∵$\frac{1}{n(n+1)(n+2)}$=$\frac{1}{2}(\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)})$.
∴$\frac{1}{1×2×3}$+$\frac{1}{2×3×4}$+…+$\frac{1}{98×99×100}$=$\frac{1}{2}[(\frac{1}{1×2}-\frac{1}{2×3})$+$(\frac{1}{2×3}-\frac{1}{3×4})$+…+$(\frac{1}{98×99}-\frac{1}{99×100})]$
=$\frac{1}{2}(\frac{1}{2}-\frac{1}{9900})$
=$\frac{4949}{19800}$.
点评 本题考查了递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
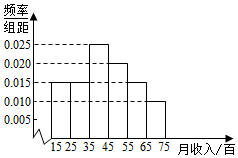 2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 500KB | B. | 1MB | C. | 2MB | D. | 4MB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com