
分析 (1)设出点C的坐标,利用$\overrightarrow{AC}$=2$\overrightarrow{CB}$,求出点C的坐标,再求模长|$\overrightarrow{OC}$|的取值范围;
(Ⅱ)求出f(x)的解析式,讨论m的取值范围,求出对应f(x)取得最小值时m的值即可.
解答 解:(1)设点C(a,b),
∵A(1,cosx),B(1+cosx,cosx),
∴$\overrightarrow{AC}$=(a-1,b-cosx),
$\overrightarrow{CB}$=(1+cosx-a,cosx-b);
又$\overrightarrow{AC}$=2$\overrightarrow{CB}$,
∴$\left\{\begin{array}{l}{a-1=2(1+cosx-a)}\\{b-cosx=2(cosx-b)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1+\frac{2}{3}cosx}\\{b=cosx}\end{array}\right.$,
∴$\overrightarrow{OC}$=(1+$\frac{2}{3}$cosx,cosx);
∴${\overrightarrow{OC}}^{2}$=${(1+\frac{2}{3}cosx)}^{2}$+cos2x
=$\frac{13}{9}$cos2x+$\frac{4}{3}$cosx+1
=$\frac{13}{9}$(cos2x+$\frac{12}{13}$cosx+$\frac{36}{169}$)-$\frac{4}{13}$+1
=$\frac{13}{9}$${(cosx+\frac{6}{13})}^{2}$+$\frac{9}{13}$;
又x∈[0,$\frac{π}{2}$],∴cosx∈[0,1],
∴当cosx=0时,${\overrightarrow{OC}}^{2}$取得最小值1,
cosx=1时,${\overrightarrow{OC}}^{2}$取得最大值$\frac{34}{9}$;
∴1≤|$\overrightarrow{OC}$|≤$\frac{\sqrt{34}}{3}$;
(Ⅱ)∵x∈[0,$\frac{π}{2}$],
∴f(x)=$\overrightarrow{OA}$•$\overrightarrow{OC}$-(2m+$\frac{2}{3}$)|$\overrightarrow{AB}$|
=(1+$\frac{2}{3}$cosx)+cos2x-(2m+$\frac{2}{3}$)$\sqrt{{(1+cosx-1)}^{2}{+(cosx-cosx)}^{2}}$
=(1+$\frac{2}{3}$cosx)+cos2x-(2m+$\frac{2}{3}$)cosx
=cos2x-2mcosx+1;
又f(x)的最小值为-$\frac{3}{2}$,cosx∈[0,1],
∴当0≤m≤1时,cosx=m,f(x)取得最小值m2-2m2+1=-$\frac{3}{2}$,解得m=$\frac{\sqrt{10}}{2}$不合题意,舍去;
当m>1时,cosx=1,f(x)取得最小值1-2m+1=-$\frac{3}{2}$,解得m=$\frac{7}{2}$;
当m<0时,cosx=0,f(x)取得最小值1≠-$\frac{3}{2}$,不合题意,舍去;
综上,实数m的值为$\frac{7}{2}$.
点评 本题考查了三角函数的求值问题,也考查了平面向量的坐标运算与数量积运算的应用问题,考查了分类讨论思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
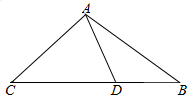 如图,在△ABC中,已知点D在BC边上,$\overrightarrow{AD}$•$\overrightarrow{AC}$=0,sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,BD=1.
如图,在△ABC中,已知点D在BC边上,$\overrightarrow{AD}$•$\overrightarrow{AC}$=0,sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,BD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | (1,$\frac{\sqrt{3}}{2}$) | D. | (1,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com