

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
分析 框图首先给变量S,k赋值S=2,k=1,然后判断k<2016是否成立,成立则执行S=$\frac{1}{1-S}$,否则跳出循环,输出S,然后依次判断执行,由执行结果看出,S的值呈周期出现,根据最后当k=2015时算法结束可求得S的值.
解答 解:框图首先给变量S,k赋值S=2,k=1.
判断1<2016,执行S=$\frac{1}{1-2}$=-1,k=1+1=2;
判断2<2016,执行S=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,k=2+1=3;
判断3<2016,执行S=$\frac{1}{1-\frac{1}{2}}$=2,k=3+1=4;
判断4<2016,执行S=$\frac{1}{1-2}$=-1,k=4+1=5;
…
程序依次执行,由上看出,程序每循环3次S的值重复出现1次.
而由框图看出,当k=2015时还满足判断框中的条件,执行循环,当k=2016时,跳出循环.
又2015=671×3+2.
所以当计算出k=2015时,算出的S的值为$\frac{1}{2}$.
此时2016不满足2016<2016,跳出循环,输出S的值为$\frac{1}{2}$.
故选:C.
点评 本题考查了循环结构的程序框图的应用,是当型结构,即先判断后执行,满足条件执行循环,不满足条件,跳出循环,算法结束,解答的关键是算准周期,属于基础题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:解答题
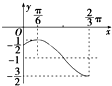 如图是函数y=Asin(ωx+ϕ)+b,(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的一段图象.求此函数解析式,并求出对称轴方程.
如图是函数y=Asin(ωx+ϕ)+b,(A>0,ω>0,|ϕ|<$\frac{π}{2}$)的一段图象.求此函数解析式,并求出对称轴方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | ¬(p∨q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
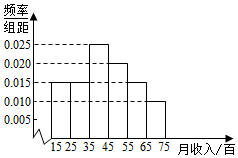 2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):
2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如表):| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {0,1,2} | C. | {-2,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com