

分析 (1)可由条件得出船的实际航行速度为7.5km/h,可用向量的知识求船的静水速度:作有向线段$\overrightarrow{AC}$表示水流速度,$\overrightarrow{AD}$表示船的实际速度,根据向量加法的平行四边形法则作平行四边形ACDE,然后由余弦定理即可求出船的静水速度;
(2)由正弦定理可求出sin∠DAE的值,从而得出cos∠DAE的值,由两角和的余弦公式即可求出cos(∠DAE+30°),即求出航行过程中船头方向与正北方向的夹角余弦值.
解答 解:(1)根据题意知,船的实际航行速度为7.5km/h;
如图,作向量$\overrightarrow{AC},\overrightarrow{AD}$,使$|\overrightarrow{AC}|=12.5,|\overrightarrow{AD}|=7.5$,$\overrightarrow{AC}$和$\overrightarrow{AE}$同向,$\overrightarrow{AD}$和$\overrightarrow{AB}$同向,连接CD,过A作CD平行线,过D作AC平行线,两平行线交于点E:则,在ADE中,AD=7.5,DE=12.5,∠ADE=120°,由余弦定理得:
AE2=AD2+DE2-2AD•DEcos120°=$7.{5}^{2}+12.{5}^{2}+2×7.5×12.5×\frac{1}{2}$=306.25;
∴AE=17.5;
∴船的静水速度为17.5km/h;
(2)由正弦定理,$\frac{DE}{sin∠DAE}=\frac{AE}{sin∠ADE}$;
即$\frac{12.5}{sin∠DAE}=\frac{17.5}{sin120°}$;
∴$sin∠ADE=\frac{5\sqrt{3}}{14}$,∴$cos∠ADE=\frac{11}{14}$;
据题意知,航行过程中船头方向与正北方向的夹角为∠DAE+30°;
∴cos(∠DAE+30°)=cos∠DAEcos30°-sin∠DAEsin30°=$\frac{11}{14}×\frac{\sqrt{3}}{2}-\frac{5\sqrt{3}}{14}×\frac{1}{2}=\frac{3\sqrt{3}}{14}$.
点评 考查用向量的方法解决实际问题的能力,向量加法的平行四边形法则,以及正余弦定理,两角和的余弦公式.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {0,1,2} | C. | {-2,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数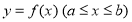 ,集合
,集合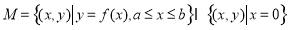 ,则集合
,则集合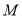 的子集的个数为( )
的子集的个数为( )
A.2 B.1或0 C.1 D.1或2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com