
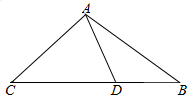
 如图,在△ABC中,已知点D在BC边上,$\overrightarrow{AD}$•$\overrightarrow{AC}$=0,sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,BD=1.
如图,在△ABC中,已知点D在BC边上,$\overrightarrow{AD}$•$\overrightarrow{AC}$=0,sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,BD=1.分析 (Ⅰ)在△ADB中,由已知结合正弦定理求得AD的长;
(Ⅱ)利用三角形一个外角等于不相邻两内角和求得sin∠ADC,进一步求得tan∠ADC,然后求解直角三角形得到AC,再由直角三角形中的面积公式求得答案.
解答 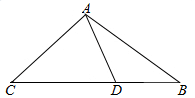 解:(Ⅰ)如图
解:(Ⅰ)如图
在△ADB中,∵sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,BD=1,
∴由正弦定理得:$\frac{AD}{sin∠ABD}=\frac{BD}{sin∠BAD}$,
∴AD=$\frac{sin∠ABD}{sin∠BAD}•BD=\frac{\frac{\sqrt{3}}{3}}{\frac{1}{3}}•1=\sqrt{3}$;
(Ⅱ)由图可知,∠ABD与∠BAD均为锐角,
∵sin∠BAD=$\frac{1}{3}$,sin∠ABD=$\frac{\sqrt{3}}{3}$,
∴cos∠BAD=$\frac{2\sqrt{2}}{3}$,cos∠ABD=$\frac{\sqrt{6}}{3}$,
∴sin∠ADC=sin(∠ABD+∠BAD)=sin∠ABDcos∠BAD+cos∠ABDsin∠BAD
=$\frac{\sqrt{3}}{3}×\frac{2\sqrt{2}}{3}+\frac{\sqrt{6}}{3}×\frac{1}{3}=\frac{\sqrt{6}}{3}$.
∵$\overrightarrow{AD}$•$\overrightarrow{AC}$=0,∴AD⊥AC,
则$cos∠ADC=\frac{\sqrt{3}}{3}$,∴$tan∠ADC=\sqrt{2}$,
∴$AC=\sqrt{2}AD=\sqrt{6}$,
∴△ADC的面积为$\frac{1}{2}×\sqrt{2}×\sqrt{6}=\sqrt{3}$.
点评 本题考查平面向量的数量积运算,考查了三角形的解法,考查数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧q | C. | ¬(p∨q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 500KB | B. | 1MB | C. | 2MB | D. | 4MB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com