
分析 取BC,AC,AD,BD的中点G,H,I,K,则AF,CE,BF,DE的中点也是HI,GH,GK,IK的中点,利用中位线定理即可证出结论.
解答 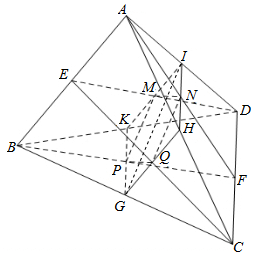 证明:设BC,AC,AD,BD的中点分别为G,H,I,K.AF,CE,BF,DE的中点分别为N,Q,P,M.连结GI.
证明:设BC,AC,AD,BD的中点分别为G,H,I,K.AF,CE,BF,DE的中点分别为N,Q,P,M.连结GI.
∴GH是△ABC的中位线,KI是△ABD的中位线,HI是△ACD的中位线,GK是△BCD的中位线.
∵AF,CE,BF,DE的中点分别为N,Q,P,M.
∴Q,N,M,P分别是GH,HI,IK,GK的中点,
连结GI,则NQ$\stackrel{∥}{=}$$\frac{1}{2}$GI,PM$\stackrel{∥}{=}$$\frac{1}{2}$GI.
∴NQ$\stackrel{∥}{=}$MP.
∴四边形PQNM是平行四边形.
点评 本题考查了三角形中位线的性质,平行四边形的判定,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:解答题
已知数列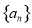 的前
的前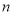 项和为
项和为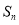 ,且
,且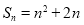 .
.
(1)证明:数列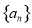 是等差数列, 并求出数列
是等差数列, 并求出数列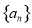 的通项公式;
的通项公式;
(2)求数列 的前
的前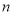 项和为
项和为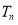 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com