
分析 (1)由向量共线的坐标运算求得Sn=bn(an-1),把bn=2代入,求出数列{an}的首项,并进一步求得数列{an}是以2为首项,以2为公比的等比数列,则通项公式可求;
(2)把bn=$\frac{n}{2}$代入Sn=bn(an-1),利用两次递推式作差可得数列{an}是公差为1的等差数列.
解答 (1)解:由$\overrightarrow{x}$=(1,bn),$\overrightarrow{y}$=(an-1,Sn),$\overrightarrow{x}$∥$\overrightarrow{y}$,
得Sn=bn(an-1),
∵bn=2,∴Sn=2(an-1).①
当n=1时,a1=2;
当n≥2时,Sn-1=2(an-1-1).②
①-②得:an=2an-2an-1,即an=2an-1,
∴数列{an}是以2为首项,以2为公比的等比数列,则${a}_{n}={2}^{n}$;
(2)证明:bn=$\frac{n}{2}$,则${S}_{n}=\frac{n}{2}({a}_{n}-1)$,即2Sn=nan-n,③
∴a1=-1,
2Sn+1=(n+1)an+1-(n+1),④
④-③得:(n-1)an+1-nan-1=0,⑤
则nan+2-(n+1)an+1-1=0,⑥
⑥-⑤得nan+2-2nan+1+nan=0,
即an+2+an=2an+1.
又a1=-1,a2=0,
∴数列{an}是公差为1的等差数列.
点评 本题考查向量共线的坐标运算,考查了数列递推式,考查等差关系的确定,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
设函数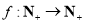 满足:对于任意大于3的正整数
满足:对于任意大于3的正整数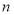 ,
,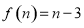 ,且当
,且当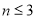 时,
时,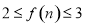 ,则不同的函数
,则不同的函数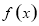 的个数为( )
的个数为( )
A.1 B.3 C.6 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{5π}{6}$ | B. | x=$\frac{7π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
定义在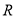 上的奇函数
上的奇函数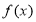 和偶函数
和偶函数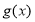 满足:
满足: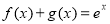 ,给出如下结论:
,给出如下结论:
① 且
且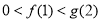 ;
;
②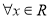 ,总有
,总有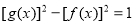 ;
;
③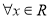 ,总有
,总有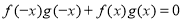 ;
;
④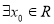 ,使得
,使得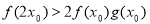 .
.
其中所有正确结论的序号是( )
A.①②③ B.②③ C.①③④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com