
分析 (1)利用中点坐标公式、相互垂直的直线斜率之间的关系即可得出;
(2)当直线过原点时,方程为 y=$\frac{1}{2}$x,当直线不过原点时,设直线的方程为:x+y=k,把点(2,1)代入直线的方程可得k值,即得所求的直线方程.
解答 解:(1)设原点(0,0)关于直线x+2y-1=0对称的点的坐标是(a,b),
则 $\left\{\begin{array}{l}{\frac{a}{2}+2•\frac{b}{2}-1=0}\\{\frac{b}{a}•(-\frac{1}{2})=-1}\end{array}\right.$,解得a=$\frac{2}{5}$,b=$\frac{4}{5}$,
∴要求的对称的点的坐标是($\frac{2}{5}$,$\frac{4}{5}$);
(2)当直线过原点时,方程为:y=$\frac{1}{2}$x,即 x-2y=0;
当直线不过原点时,设直线的方程为:x+y=k,
把点(2,1)代入直线的方程可得 k=3,
故直线方程是 x+y-3=0.
综上可得所求的直线方程为:x-2y=0,或 x+y-3=0,
故答案为:($\frac{2}{5}$,$\frac{4}{5}$);x-2y=0,或 x+y-3=0.
点评 本题考查中点坐标公式、相互垂直的直线斜率之间的关系以及用待定系数法求直线方程,体现了分类讨论的数学思想,注意不要漏掉当直线过原点时的情况.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
在一个港口,相邻两次高潮发生的时间相距 ,低潮时水深为
,低潮时水深为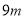 ,高潮时水深为
,高潮时水深为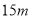 .每天潮涨潮落时,该港口水的深度
.每天潮涨潮落时,该港口水的深度 (
( )关于时间
)关于时间 (
( )的函数图象可以近似地看成函数
)的函数图象可以近似地看成函数 的图象,其中
的图象,其中 ,且
,且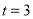 时涨潮到一次高潮,则该函数的解析式可以是( )
时涨潮到一次高潮,则该函数的解析式可以是( )
A.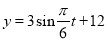 B.
B.
C.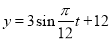 D.
D.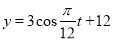
查看答案和解析>>
科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是( )
,则它的表面积是( )
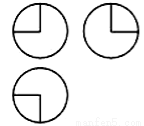
A.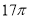 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com