练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知以点P为圆心的圆经过点A（1，4），B（3，6），线段AB的垂直平分线与圆交于点C，D，且CD=4．
    （1）求直线CD的方程；
    （2）求圆P的方程．

    分析 （1）先求得直线AB的斜率和AB的中点，进而求得CD斜率，利用点斜式取得直线CD 方程．
    （2）设出圆心P的坐标，利用直线方程列方程，利用点到直线的距离确定a和b的等式综合求得a和b，则圆的方程可得．

    解答 解：（1）直线AB的斜率k=1，AB中点坐标为（2，5），
    ∴直线CD的斜率为-1，
    ∴直线CD方程为y-5=-（x-2），即x+y-7=0
    （2）设圆心P（a，b），则由P在CD上，得a+b-7=0①
    又直径|CD|=4，∴|PA|=2，（a-1）2+（b-4）2=4②
    由①②解得a=3，b=4或a=1，b=6
    ∴圆心P（3，4）或P（1，6），
    ∴圆P的方程为（x-3）2+（y-4）2=4或（x-1）2+（y-6）2=4．

    点评 本题主要考查了直线与圆的方程的应用．考查了学生基础知识的综合运用能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

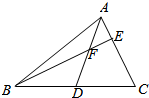    13．△ABC中，D为BC的中点，E为AC边上靠近点A的一个三等分点，AD与BE交于点F，求：
    （1）AF与FD的长度之比；
    （2）BF与FE的长度之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．（1）已知二次函数h（x）与x轴的两交点坐标为（-2，0），（3，0），且h（0）=-3，求h（x）；
    （2）已知f（x+1）=x2-2x，求f（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=$\frac{2{x}^{2}-kx+k}{{e}^{x}}$．
    （1）当k为何值时，f（x）在R上是减函数；
    （2）试确定实数k的值，使f（x）的极小值为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．数列{an}前n项和为Sn，且an=$\frac{1}{2}$（3n+Sn），n∈N*．
    （1）求{an}的通项公式an．
    （2）{an}中是否存在二项构成等差数列；若存在，求出一组；若不存在，说明理由．
    （3）令bn=$\frac{3}{{a}_{n}}$，求证：b1+b2+…+bn＜2．（n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）是定义R上的奇函数，在[0，+∞）上为增函数，若f（1-a）+f（$\frac{1}{2}$-2a）＜0，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．求下列函数的解析式：
    （1）已知f（x）是二次函数且f（0）=2，f（2-x）-f（x）=0，f（1）=-2，求f（x）；
    （2）已知f（$\sqrt{x}$+1）=x+3，求f（x）；
    （3）已知f（x）-2f（$\frac{1}{x}$）=3x+2，求f（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知关于x的不等式ax2+bx+c＞0的解集是{x|x＞2或x＜$\frac{1}{2}$}，求关于x的不等式ax2-bx+c≤0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=x2+2x．
    （1）求f（2），f（a+1）（a∈R）的值；
    （2）证明函数f（x）在[-1，+∞）上是增函数．

    查看答案和解析>>

    同步练习册答案