
【题目】如图,在△ABC中,AB=2,cosB= ![]() ,点D在线段BC上.
,点D在线段BC上. 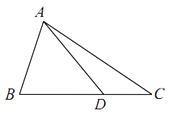
(1)若∠ADC= ![]() π,求AD的长;
π,求AD的长;
(2)若BD=2DC,△ABC的面积为 ![]()
![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)在三角形中,∵cosB= ![]() ,∴sinB=
,∴sinB= ![]() .
.
在△ABD中,由正弦定理得 ![]() ,
,
又AB=2, ![]() ,sinB=
,sinB= ![]() .
.
∴AD= ![]()
(2)∵BD=2DC,∴S△ABD=2S△ADC,S△ABC=3S△ADC,
又 ![]() ,∴
,∴ ![]() ,
,
∵S△ABC= ![]() ,∴BC=6,
,∴BC=6,
∵ ![]() ,
, ![]() ,
,
S△ABD=2S△ADC,∴ ![]() ,
,
在△ABC中,由余弦定理得:
AC2=AB2+BC2﹣2ABBCcos∠ABC,∴AC=4 ![]() ,
,
∴ ![]() =2
=2 ![]() =4
=4 ![]()
【解析】(1)求出sinB= ![]() ,由正弦定理得
,由正弦定理得 ![]() ,由此能求出AD.(2)推导出S△ABD=2S△ADC , S△ABC=3S△ADC ,
,由此能求出AD.(2)推导出S△ABD=2S△ADC , S△ABC=3S△ADC , ![]() ,BC=6,从而得到
,BC=6,从而得到 ![]() ,由此利用余弦定理能求出
,由此利用余弦定理能求出 ![]() 的值.
的值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
(Ⅰ)证明:SD⊥平面SAB;
(Ⅱ)求AB与平面SBC所成的角的大小.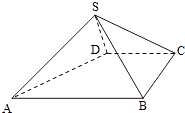
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=1,E,F分别是CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:AB⊥AC;
(2)证明:DF⊥AE;
(3)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不恒为零的函数f(x)在定义域[0,1]上的图象连续不间断,满足条件f(0)=f(1)=0,且对任意x1 , x2∈[0,1]都有|f(x1)﹣f(x2)|≤ ![]() |x1﹣x2|,则对下列四个结论: ①若f(1﹣x)=f(x)且0≤x≤
|x1﹣x2|,则对下列四个结论: ①若f(1﹣x)=f(x)且0≤x≤ ![]() 时,f(x)=
时,f(x)= ![]() x(x﹣
x(x﹣ ![]() ),则当
),则当 ![]() <x≤1时,f(x)=
<x≤1时,f(x)= ![]() (1﹣x)(
(1﹣x)( ![]() ﹣x);
﹣x);
②若对x∈[0,1]都有f(1﹣x)=﹣f(x),则y=f(x)至少有3个零点;
③对x∈[0,1],|f(x)|≤ ![]() 恒成立;
恒成立;
④对x1 , x2∈[0,1],|f(x1)﹣f(x2)|≤ ![]() 恒成立.
恒成立.
其中正确的结论个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣
(α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣ ![]() )=2
)=2 ![]() (Ⅰ)将直线l化为直角坐标方程;
(Ⅰ)将直线l化为直角坐标方程;
(Ⅱ)求曲线C上的一点Q 到直线l 的距离的最大值及此时点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ![]() .
.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示,BO是梯形ABCD的高,∠BAD=45°,OB=BC=1,OD=3OA,现将梯形ABCD沿OB折起如图乙所示的四棱锥P﹣OBCD,使得PC= ![]() ,点E是线段PB上一动点.
,点E是线段PB上一动点. 
(1)证明:DE和PC不可能垂直;
(2)当PE=2BE时,求PD与平面CDE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com