A
分析:由已知中函数的解析式,我们易求出f(x)与y=m的交点情况为:当a<-3,或a>1时,有一个交点;当a=-3,或a=1时,有两个交点;当-3<a<1时,有三个交点;g(x)与y=a点情况为(x)与y=a的交点情况为:当0<a<1时有两个交点,一个在区间(-4,-3)上,一个在区间(-3,-2)上;当a=1时有两个交点,一个为-3,一个为

;当a>1时有两个交点,一个在区间(0,

)上,一个在区间(

-,1)上.分类讨论后,即可得到方程g[f(x)]-a=0(a为正实数)的根的个数所有的情况,进而得到答案.
解答:∵函数f(x)=x
3-3x
2+1,g(x)=
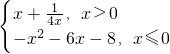
,
∴当a=1时,若方程g[f(x)]-a=0,则:
f(x)=-3,此时方程有2个根
或f(x)=

,此时方程有3个根
故方程g[f(x)]-a=0可能共有5个根;
当0<a<1时,方程g[f(x)]-a=0,则:
f(x)∈(-4,-3),此时方程有1个根
或f(x)∈(-3,-2),此时方程有3个根
故方程g[f(x)]-a=0可能共有4个根;
当a>1时,方程g[f(x)]-a=0,则:
可能有4个、5个或6个根.
故选A.
点评:本题考查的知识点是根的存在性及根的个数判断,其中分析内外函数的图象是解答本题的关键.

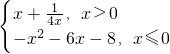 ,则方程g[f(x)]-a=0(a为正实数)的根的个数不可能 为
,则方程g[f(x)]-a=0(a为正实数)的根的个数不可能 为 ;当a>1时有两个交点,一个在区间(0,
;当a>1时有两个交点,一个在区间(0, )上,一个在区间(
)上,一个在区间( -,1)上.分类讨论后,即可得到方程g[f(x)]-a=0(a为正实数)的根的个数所有的情况,进而得到答案.
-,1)上.分类讨论后,即可得到方程g[f(x)]-a=0(a为正实数)的根的个数所有的情况,进而得到答案.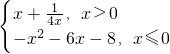 ,
, ,此时方程有3个根
,此时方程有3个根

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<