
分析 记正品为A,B,C,次品为a,b,现从5件产品中任取2件,列举出所有的基本事件,再分别找到满足条件的基本事件,根据概率公式计算即可.
解答 解:记正品为A,B,C,次品为a,b,现从5件产品中任取2件,所有的基本事件有Ω={AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab}共10个,
(1)记事件A=“恰有一件次品”,则A={Aa,Ab,Ba,Bb,Ca,Cb}共有6个,故P(A)=$\frac{6}{10}$=$\frac{3}{5}$,
(2)记事件B=“至少有一件正品”,则B={AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb}共有9个,故P(B)=$\frac{9}{10}$,
(3)记事件C=“至多有一件正品”,则B={Aa,Ab,Ba,Bb,Ca,Cb,ab}共有7个,故P(C)=$\frac{7}{10}$.
点评 本题考查了古典概型概率的问题,关键是列举,属于基础题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:选择题
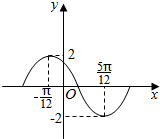
| A. | A=2,ω=2,φ=$\frac{π}{3}$ | B. | A=2,ω=2,φ=$\frac{2π}{3}$ | C. | A=2,ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ | D. | A=2,ω=2,φ=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一年级 | 二年级 | 三年级 | |
| 男生 | A | B | C |
| 女生 | X | Y | Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (2,4) | C. | (4,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
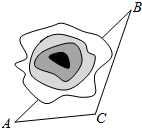 如图,在铁路建设中需要确定隧道的长度和隧道两端的施工方向,已测得隧道两端的两点A,B到某一点C的距离分别为2千米,2$\sqrt{3}$千米及∠ACB=150°,则A,B两点间的距离为2$\sqrt{7}$千米.
如图,在铁路建设中需要确定隧道的长度和隧道两端的施工方向,已测得隧道两端的两点A,B到某一点C的距离分别为2千米,2$\sqrt{3}$千米及∠ACB=150°,则A,B两点间的距离为2$\sqrt{7}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com