
分析 先求导,再分类讨论,根据函数的单调性和最值得关系即可判断.
解答 解:∵f(x)=ax+$\frac{b}{x}$,
∴f′(x)=a-$\frac{b}{{x}^{2}}$=$\frac{a{x}^{2}-b}{{x}^{2}}$=$\frac{a({x}^{2}-\frac{b}{a})}{{x}^{2}}$,
(1)当ab<0时,
当a>0,b<0时,f(x)在(-∞,0),(0,+∞)上单调递增,
∴f(x)在[1,2]单调递增,
∴f(x)min=2=f(1)=a+b,即b=2-a,
当a<0,b>0时,f(x)在(-∞,0),(0,+∞)上单调递减,
∴f(x)在[1,2]单调递减,
∴f(x)min=2=f(2)=2a+$\frac{b}{2}$,即b=4-4a,
(2)当ab>0时,
令f′(x)=0,解得x=±$\sqrt{\frac{b}{a}}$,
当a>0,b>0时,f(x)在(-∞,-$\sqrt{\frac{b}{a}}$),($\sqrt{\frac{b}{a}}$,+∞)上单调递增,在(-$\sqrt{\frac{b}{a}}$,0),(0,$\sqrt{\frac{b}{a}}$)单调递减,
当$\sqrt{\frac{b}{a}}$<1时,即$\frac{b}{a}$<1时,
∴f(x)在[1,2]单调递增,
∴f(x)min=2=f(1)=a+b,即b=2-a,
当$\sqrt{\frac{b}{a}}$>2时,即$\frac{b}{a}$>4时,
∴f(x)在[1,2]单调递减,
∴f(x)min=2=f(2)=2a+$\frac{b}{2}$,即b=4-4a,
当1≤$\sqrt{\frac{b}{a}}$≤2时,即1≤$\frac{b}{a}$≤4时,
∴f(x)在[1,$\sqrt{\frac{b}{a}}$]单调递减,在($\sqrt{\frac{b}{a}}$,2]上单调递增,
∴f(x)min=2=f($\sqrt{\frac{b}{a}}$)=a•$\sqrt{\frac{b}{a}}$+$\frac{b}{\sqrt{\frac{b}{a}}}$=2,即b=$\frac{1}{a}$,
当a<0,b<0时,f(x)在(-∞,-$\sqrt{\frac{b}{a}}$),($\sqrt{\frac{b}{a}}$,+∞)上单调递减,在(-$\sqrt{\frac{b}{a}}$,0),(0,$\sqrt{\frac{b}{a}}$)单调递增,
当$\sqrt{\frac{b}{a}}$<1时,即$\frac{b}{a}$<1时,
∴f(x)在[1,2]单调递减,
∴f(x)min=2=f(2)=2a+$\frac{b}{2}$,即b=4-4a,
当$\sqrt{\frac{b}{a}}$>2时,即$\frac{b}{a}$>4时,
∴f(x)在[1,2]单调递增,
∴f(x)min=2=f(1)=a+b,即b=2-a,
当1≤$\sqrt{\frac{b}{a}}$≤2时,即1≤$\frac{b}{a}$≤4时,
∴f(x)在[1,$\sqrt{\frac{b}{a}}$]单调递增,在($\sqrt{\frac{b}{a}}$,2]上单调递减,
∵f(1)=a+b,f(2)=2a+$\frac{b}{2}$,
当1≤$\frac{b}{a}$≤2时,f(1)≥f(2),f(x)min=2=f(2)=2a+$\frac{b}{2}$,即b=4-4a,
当2<$\frac{b}{a}$≤4,f(1)≤f(2),f(x)min=2=f(1)=a+b,即b=2-a,
综上所述:②正确,①③④其余不正确
故答案为:②
点评 本题考查了函数的单调性质和函数的最值得关系,关键是分类,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
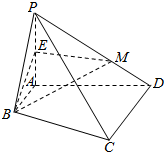 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
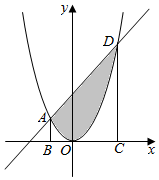 如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )
如图所示,直线x-y+2=0与抛物线y=x2相交于A,D两点,分别过A,D作平行于y轴的直线交x轴于B,C两点,随机向梯形ABCD内投一点P,则点P落在抛物线弓形AOD内(图中阴影部分)的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com