
【题目】已知![]() ,函数
,函数![]()
(1)讨论![]() 的单调区间和极值;
的单调区间和极值;
(2)将函数![]() 的图象向下平移1个单位后得到
的图象向下平移1个单位后得到![]() 的图象,且
的图象,且![]() 为自然对数的底数)和
为自然对数的底数)和![]() 是函数
是函数![]() 的两个不同的零点,求
的两个不同的零点,求![]() 的值并证明:
的值并证明: ![]() 。
。
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)求出函数f(x)的定义域,求导数得f ′(x)=![]() ,进而通过导数的正负得单调区间及极值;
,进而通过导数的正负得单调区间及极值;
(2)利用g(x)=mx﹣lnx,且x1=![]() 是函数g(x)的零点,推出m值,利用函数的零点判定定理,结合函数g(x)在(2
是函数g(x)的零点,推出m值,利用函数的零点判定定理,结合函数g(x)在(2![]() ,+∞)上单调递增,即可证得.
,+∞)上单调递增,即可证得.
试题解析:
解:(1)函数f(x)的定义域为(0,+∞).求导得f ′(x)=m-![]() =
=![]() .
.
①若m≤0,则f ′(x)<0,f(x)是(0,+∞)上的减函数,无极值;
②若m>0,令f ′(x)=0,得x=![]() .
.
当x∈(0, ![]() )时,f ′(x)<0,f(x)是减函数;
)时,f ′(x)<0,f(x)是减函数;
当x∈(![]() ,+∞)时,f ′(x)>0,f(x)是增函数.
,+∞)时,f ′(x)>0,f(x)是增函数.
所以当x=![]() 时,f(x)有极小值,极小值为f(
时,f(x)有极小值,极小值为f(![]() )=2—ln
)=2—ln![]() =2+lnm.
=2+lnm.
综上所述,当m≤0时,f(x)的递减区间为(0,+∞),无极值;当m>0时,f(x)的递增区间为(![]() ,+∞),递减区间为(0,
,+∞),递减区间为(0, ![]() ),极小值为2+lnm
),极小值为2+lnm
(2)因为![]() ,且x1=
,且x1=![]() 是函数g(x)的零点,
是函数g(x)的零点,
所以g(![]() )=0,即m
)=0,即m![]() —
—![]() =0,解得m=
=0,解得m=![]() .
.
所以g(x)=![]() -lnx. 因为g(e
-lnx. 因为g(e![]() )=
)=![]() -
-![]() <0,g(e
<0,g(e![]() )=
)=![]() -
-![]() >0,
>0,
所以g(e![]() )g(e
)g(e![]() )<0.
)<0.
由(1)知,函数g(x)在(2![]() ,+∞)上单调递增,
,+∞)上单调递增,
所以函数g (x)在区间(e![]() ,e
,e![]() )上有唯一零点,
)上有唯一零点,
因此x2>e![]() ,即x2>
,即x2>![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
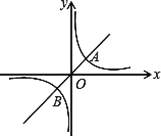
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},an≥0,a1=0,an+12+an+1﹣1=an2(n∈N).记Sn=a1+a2+…+an . Tn= ![]() +
+ ![]() +…+
+…+ ![]() .求证:当n∈N*时
.求证:当n∈N*时
(1)0≤an<an+1<1;
(2)Sn>n﹣2;
(3)Tn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.

(1)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某高中甲、乙两个班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.

(1)甲班和乙班同学身高的中位数各是多少?并计算甲班样本的方差.
(2)现从乙班这10名同学中随机抽取2名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
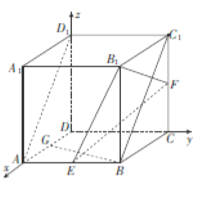
【题目】如图,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 上一点,且异面直线
上一点,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
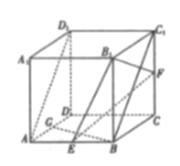
(1)证明: ![]() 为
为![]() 的中点;
的中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,不妨令正方体的棱长为2,设
,不妨令正方体的棱长为2,设![]() ,利用
,利用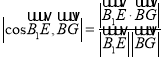 ,解得
,解得![]() ,即可证得;
,即可证得;
(2)分别求得平面![]() 与平面
与平面![]() 的法向量
的法向量![]() ,利用
,利用![]() 求解即可.
求解即可.
试题解析:
(1)证明:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .
.
不妨令正方体的棱长为2,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
所以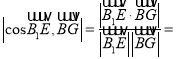
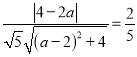 ,
,
所以![]() ,解得
,解得![]() (
(![]() 舍去),即
舍去),即![]() 为
为![]() 的中点.
的中点.
(2)解:由(1)可得![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则![]() .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以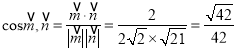 .
.
所以所求锐二面角的余弦值为![]() .
.
点睛:空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.
【题型】解答题
【结束】
22
【题目】已知椭圆![]() 的短轴长为2,且椭圆
的短轴长为2,且椭圆![]() 过点
过点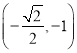 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 过定点
过定点![]() ,且斜率为
,且斜率为![]() ,若椭圆
,若椭圆![]() 上存在
上存在![]() 两点关于直线
两点关于直线![]() 对称,
对称, ![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围及
的取值范围及![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com