练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．如图都是边长为1的正方体叠成的几何体，例如第（1）个几何体的表面积为6个平方单位，第（2）个几何体的表面积为18个平方单位，第（3）个几何体的表面积是36个平方单位．依此规律，则第n个几何体的表面积是3n（n+1）个平方单位．

    分析 结合图形，发现第（1）个图形的表面积是1×6=6，第（2）个图形的表面积是（1+2）×6=18，第（3）图形的表面积是（1+2+3）×6=36；以此类推即可求解．

    解答 解：结合图形，发现：
    第（1）个图形的表面积是1×6=6，
    第（2）个图形的表面积是（1+2）×6=18，
    第（3）图形的表面积是（1+2+3）×6=36，
    第（4）图形的表面积是（1+2+3+4）×6=60，
    …
    故第n个图形的表面积是（1+2+3+…+n）×6=3n（n+1）
    故答案为：3n（n+1）

    点评 本题考查的知识点是归纳推理，其中从已知中的四个图形中，找出其表面积的变化规律，并进行大胆推断，是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知2cos2x+sin2x=Asin（ωx+φ）+b（A＞0，0＜φ＜π），则A，φ，b的值分别为（　　）
    A．$A=2，φ=\frac{π}{4}，b=1$B．$A=\sqrt{2}，φ=\frac{π}{6}，b=2$C．$A=\sqrt{2}，φ=\frac{π}{6}，b=1$D．$A=\sqrt{2}，φ=\frac{π}{4}，b=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图是某社区的部分规划设计图，住宅区一边的边界曲线记为C，步行街（宽度不计）所在直线L与曲线C相切于点M，以点E为圆心，1百米为半径的圆的四分之一为大型超市，为方便住宅区居民购物休闲，该社区计划在步行街与大型超市之间铺设一条连接道路AB（宽度不计）以及修建花园广场．
    根据相关数据，某同学建立了平面直角坐标系xOy，曲线C用函数模型y=ex-1+kx+b（k，b为常数）拟合．并求得直线l：y=2x，M（1，2），E（2$\sqrt{5}$，0），单位：百米．点A在l上，点B在$\widehat{FG}$上
    （1）求曲线C的方程和AB的最短距离；
    （2）若过点A作AP垂直于x轴，垂足为P，在空地△APB内截取一个面积最大的矩形，用来修建一个花园广场．要求矩形的一边在AB上．在连接道路AB最短时，求花园广场的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

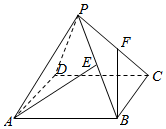    20．已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（　　）
    A．$\frac{{\sqrt{3}}}{3}$B．$\frac{{\sqrt{6}}}{3}$C．$\frac{1}{6}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在平面直角坐标系xOy中，F是抛物线C：y2=2px（p＞0）的焦点，M是抛物线C上的任意一点，当M位于第一象限内时，△OFM外接圆的圆心到抛物线C准线的距离为$\frac{3}{2}$．
    （1）求抛物线C的方程；
    （2）过K（-1，0）的直线l交抛物线C于A，B两点，且$\overrightarrow{KA}=λ\overrightarrow{KB}（λ∈[2，3]）$，点G为x轴上一点，且|GA|=|GB|，求点G的横坐标x0的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设S是不等式x2-x-6≤0的解集，整数m、n∈S．
    （1）求“m+n=0”的概率；
    （2）设ξ=m2，求ξ的分布列及其数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知x＞0，y＞0，且xy-x-y=3．
    （1）求xy的最小值；
    （2）求x+y的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在正四面体P-ABC体积为V，现内部取一点S，则$\frac{V}{3}＜{V_{S-ABC}}＜\frac{V}{2}$的概率为（　　）
    A．$\frac{37}{216}$B．$\frac{8}{27}$C．$\frac{91}{216}$D．$\frac{13}{27}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知f（x）、g（x）都是定义在R上的函数，g（x）≠0，f'（x）g（x）＜f（x）g'（x），f（x）=axg（x），$\frac{f（1）}{g（1）}+\frac{f（-1）}{g（-1）}=\frac{5}{2}$，在有穷数列$\left\{{\frac{f（n）}{g（n）}}\right\}$（n=1，2，…，10）中，任意取前k项相加，则前k项和不小于$\frac{63}{64}$的k的取值范围是（　　）
    A．[6，10]且k∈N*B．（6，10]且k∈N*C．[5，10]且k∈N*D．[1，6]且k∈N*

    查看答案和解析>>

    同步练习册答案