解析:(Ⅰ)∵a
n+1-S
n-1=0①
∴n≥2时,a
n-S
n-1-1=0②
①─②得:

(n≥2)(2分)
由a
n+1-2S
n-1=0及a
1=1得a
2-S
1-1=0?a
2=S
1+1=a
1+1=2
∴{a
n}是首项为1,公比为2的等比数列,
∴a
n=2
n-1(4分)
(Ⅱ)解法一:由(Ⅰ)知

(5分)
若{S
n+λ•n-λ•2
n}为等差数列,
则S
1+λ-2λ,S
2+2λ-4λ,S
3+3λ-8λ则成等差数列,(6分)
∴(S
1-λ)+(S
3-5λ)=2(S
2-2λ)?8-6λ=6-4λ,∴λ=1(8分)
当λ=1时,S
n+λ•n-λ•2
n=S
n+n-2
n=n-1,显然{n-1}成等差数列,
∴存在实数λ=1,使得数列{S
n+λ•n-λ•2
n}成等差数列.(9分)
解法二:由(Ⅰ)知

(5分)
∴S
n+λ•n-λ•2
n=(2
n-1)+λ•n-λ•2
n=λ•n-1+(1-λ)•2
n(7分)
要使数列{S
n+λ•n-λ•2
n}成等差数列,则只须1-λ=0,即λ=1即可.(8分)
故存在实数λ=1,使得数列{S
n+λ•n-λ•2
n}成等差数列.(9分)
(Ⅲ)∵
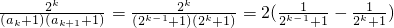
(10分)
∴
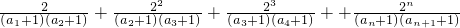
=
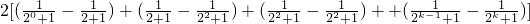
=
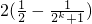
(12分)
∵
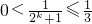
,
∴
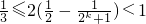
,
∴
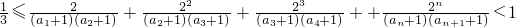
(14分)
分析:(Ⅰ)由题设条件知

(n≥2),a
2=S
1+1=a
1+1=2,由此可知a
n=2
n-1.
(Ⅱ)若{S
n+λ•n-λ•2
n}为等差数列,则S
1+λ-2λ,S
2+2λ-4λ,S
3+3λ-8λ则成等差数列,由此能推出λ=1.由此可知存在实数λ=1,使得数列{S
n+λ•n-λ•2
n}成等差数列.
(Ⅲ)由
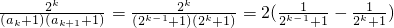
入手,可得证.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

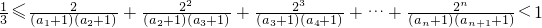 .
. (n≥2)(2分)
(n≥2)(2分) (5分)
(5分) (5分)
(5分)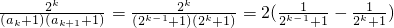 (10分)
(10分)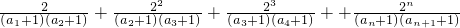
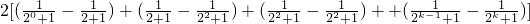
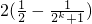 (12分)
(12分)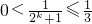 ,
,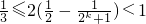 ,
,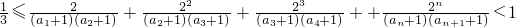 (14分)
(14分) (n≥2),a2=S1+1=a1+1=2,由此可知an=2n-1.
(n≥2),a2=S1+1=a1+1=2,由此可知an=2n-1.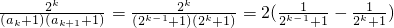 入手,可得证.
入手,可得证.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案