
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过点C.已知AB=3 m,AD=2 m.
(1) 要使矩形AMPN的面积大于32 m2,则AN的长应在什么范围内?
(2) 当AN的长度是多少时,矩形AMPN的面积最小?并求最小面积.
(3) 若AN的长度不少于6 m,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
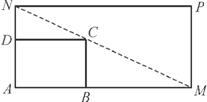
(1) 设AN=x m(x>2),则ND=x-2.
因为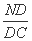 =
=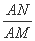 ,即
,即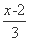 =
=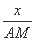 ,所以AM=
,所以AM=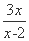 .
.
因为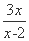 ·x>32,所以3x2-32x+64>0,即(3x-8)(x-8)>0,
·x>32,所以3x2-32x+64>0,即(3x-8)(x-8)>0,
所以2<x<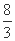 或x>8.
或x>8.
即满足题意的AN的取值范围为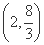 ∪(8,+∞).
∪(8,+∞).
(2) S矩形AMPN=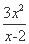
=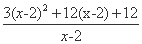
=3(x-2)+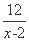 +12
+12
≥2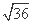 +12=24,
+12=24,
当且仅当x=4时取等号,即当AN=4m时,矩形AMPN的面积最小,最小面积为24 m2.
(3) 因为S矩形AMPN=3(x-2)+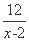 +12(x≥6),
+12(x≥6),
令x-2=t(t≥4),则f(t)=3t+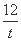 +12.
+12.
因为f'(t)=3-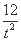 ,当t≥4时,f'(t)>0,
,当t≥4时,f'(t)>0,
所以f(t)=3t+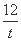 +12在[4,+∞)上单调递增,
+12在[4,+∞)上单调递增,
所以f(t)min=f(4)=27,此时x=6.
故当AN的长度是6 m时,矩形AMPN的面积最小,最小面积为27 m2.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,已知椭圆C: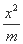 +
+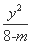 =1.
=1.
(1) 若椭圆C的焦点在x轴上,求实数m的取值范围;
(2) 已知m=6.
①若P是椭圆C上的动点,点M的坐标为(1,0),求PM的最小值及对应的点P的坐标;
②过椭圆C的右焦点F作与坐标轴不垂直的直线,交椭圆C于A,B两点,线段AB的垂直平分线l交x轴于点N,求证: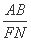 是定值;并求出这个定值.
是定值;并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com