
设 是一个自然数,
是一个自然数, 是
是 的各位数字的平方和,定义数列
的各位数字的平方和,定义数列 :
: 是自然数,
是自然数, (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求证:
,求证: ;
;
(3)当 时,求证:存在
时,求证:存在 ,使得
,使得 .
.
(1) ,
, ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.
解析试题分析:本题是一道新定义题,主要考查归纳推理、数学归纳法、分类讨论思想等基础知识,考查学生的分析问题解决问题的能力和转化能力.第一问,由于 是a的各位数字的平方和,所以
是a的各位数字的平方和,所以 ,
, ;第二问,通过题干中给出的
;第二问,通过题干中给出的 的定义设出
的定义设出 的值,利用
的值,利用 ,得到
,得到 的值,然后用作差法比较
的值,然后用作差法比较 和
和 的大小;第三问,由已知条件
的大小;第三问,由已知条件
 ,由于
,由于 且
且 ,得
,得 ,由归纳推理得
,由归纳推理得 ,再用数学归纳法证明一下,因此存在
,再用数学归纳法证明一下,因此存在 (
( ),有
),有 ,再分类讨论p、q的情况,得出结论.
,再分类讨论p、q的情况,得出结论.
(1) ;
; . 5分
. 5分
(2)假设 是一个
是一个 位数(
位数( ),
),
那么可以设 ,
,
其中 且
且 (
( ),且
),且 .
.
由 可得,
可得, .
. 所以
所以 .
.
因为 ,所以
,所以 .
.
而 ,
,
所以 ,即
,即 . 9分
. 9分
(3)由 ,即
,即 ,可知
,可知 .
.
同理 ,可知
,可知 .
.
由数学归纳法知,对任意 ,有
,有 .
.
即对任意 ,有
,有 .
.
因此,存在 (
( ),有
),有 .
.
则 ,
, , ,
, , ,
,
可得对任意 ,
, ,有
,有 .
.
设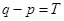 ,即对任意
,即对任意 ,有
,有 .
.
若 ,取
,取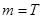 ,
, ,则有
,则有 .
.
若 ,由
,由 ,可得
,可得 ,
,
取 ,
, ,则有
,则有 . 14分
. 14分
考点:归纳推理、数学归纳法、分类讨论思想.


科目:高中数学 来源: 题型:解答题
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.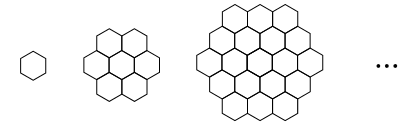
(1)试给出f(4),f(5)的值,并求f(n)的表达式(不要求证明);
(2)证明: +
+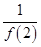 +
+ +…+
+…+ <
< .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列 的前
的前 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取 个数,其所有可能的
个数,其所有可能的 个数的乘积的和为
个数的乘积的和为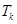 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,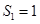 ;当
;当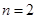 时,
时, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想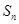 ,并用数学归纳法证明.
,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于平面上的点集 ,如果连接
,如果连接 中任意两点的线段必
中任意两点的线段必
定包含于 ,则称
,则称 为平面上的凸集,给出平面上4个
为平面上的凸集,给出平面上4个
点集的图形如右(阴影区域及其边界):其中为凸集
的是 (写出所有凸集相应图形的序号)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知下列三个方程:x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0,其中至少有一个方程有实根,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com