Question

4．${x^2}-{log_a}（x+1）＜2x-1在（\frac{1}{2}，1）$内恒成立，则a的取值范围是（　　）

• A． $[{（{\frac{3}{2}}）^{-4}}，1）$
• B． $（{（{\frac{3}{2}}）^{-4}}，1）$
• C． $（1，{（{\frac{3}{2}}）^4}）$
• D． $（1，{（{\frac{3}{2}}）^4}]$

Answer 1

分析 把已知不等式变形，得到x²-2x+1＜log_a（x+1）在（$\frac{1}{2}，1$）内恒成立，令f（x）=x²-2x+1，g（x）=log_a（x+1），由f（$\frac{1}{2}$）=g（$\frac{1}{2}$）求得a值，画出两个函数图象，数形结合可得a的取值范围．

解答 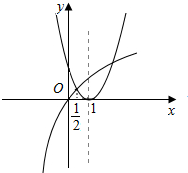解：由x²-log_a（x+1）＜2x-1在（$\frac{1}{2}，1$）内恒成立，得
x²-2x+1＜log_a（x+1）在（$\frac{1}{2}，1$）内恒成立，
令f（x）=x²-2x+1，g（x）=log_a（x+1），
作出两个函数的图象如图：
∵f（$\frac{1}{2}$）=$\frac{1}{4}$，g（$\frac{1}{2}$）=$lo{g}_{a}\frac{3}{2}$，
∴由f（$\frac{1}{2}$）=g（$\frac{1}{2}$），得$lo{g}_{a}\frac{3}{2}=\frac{1}{4}$，
∴${a}^{\frac{1}{4}}=\frac{3}{2}$，则$a=（\frac{3}{2}）^{4}$．
∴要使${x^2}-{log_a}（x+1）＜2x-1在（\frac{1}{2}，1）$内恒成立，
则a的取值范围是$（1，（\frac{3}{2}）^{4}]$．
故选：D．

点评 本题考查函数恒成立问题，考查了数学转化思想方法和数形结合的解题思想方法，是中档题．