
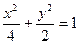 上动点
上动点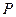 到定点
到定点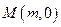 ,其中
,其中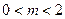 的距离
的距离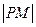 的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线
的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线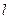 ,使
,使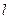 与椭圆C的两个交点A、B满足条件
与椭圆C的两个交点A、B满足条件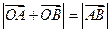 (O为原点),若存在,求出
(O为原点),若存在,求出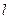 的方程,若不存在请说是理由。
的方程,若不存在请说是理由。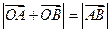 知
知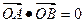 从而将条件转化点的坐标运算再结合韦达定理解答。
从而将条件转化点的坐标运算再结合韦达定理解答。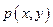 ,由
,由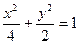 得
得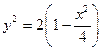 故
故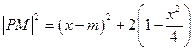
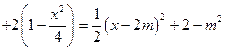 由于
由于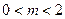 且
且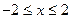 故当
故当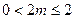 时,
时,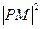 的最小值为
的最小值为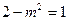 此时
此时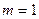 ,当
,当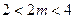 时,
时,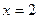 取得最小值为
取得最小值为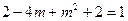 解得
解得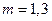 不合题意舍去。综上所知当
不合题意舍去。综上所知当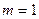 是满足题意此时M的坐标为(1,0)。
是满足题意此时M的坐标为(1,0)。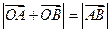 等价于
等价于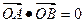 ,当
,当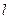 的斜率不存在时,
的斜率不存在时,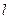 与C的交点为
与C的交点为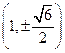 ,此时
,此时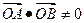 ,设
,设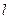 的方程为
的方程为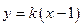 ,代入椭圆方程整理得
,代入椭圆方程整理得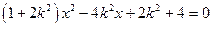 ,由于点M在椭圆内部故
,由于点M在椭圆内部故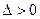 恒成立,由
恒成立,由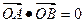 知
知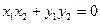 即
即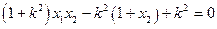 ,据韦达定理得
,据韦达定理得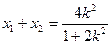 ,
,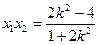 代入上式得
代入上式得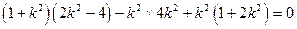 得
得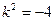 不合题意。综上知这样的直线不存在。
不合题意。综上知这样的直线不存在。

科目:高中数学 来源:不详 题型:解答题
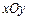 中,
中,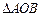 和
和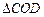 为两等腰直角三角形,
为两等腰直角三角形,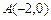 ,C(a,0)(a>0).设
,C(a,0)(a>0).设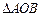 和
和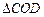 的外接圆圆心分别为
的外接圆圆心分别为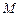 ,
,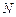 .
.
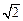 ,若存在,求此时⊙N的标准方程;若不存在,说明理由.
,若存在,求此时⊙N的标准方程;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com