
分析 直线l:mx-y-1=0经过定点P(0,-1).利用斜率计算公式可得:kPA,kPB.由于直线l:mx-y-1=0与线段AB相交,可得kPA≥m≥kPB.即可得出.
解答 解:直线l:mx-y-1=0经过定点P(0,-1).
kPA=$\frac{-1-1}{0-1}$=2,kPB=$\frac{-1-2}{0-4}$=$\frac{3}{4}$.
∵直线l:mx-y-1=0与线段AB相交,
∴kPA≥m≥kPB.
∴2≥m≥$\frac{3}{4}$.
∴实数m的取值范围为[$\frac{3}{4}$,2],
故答案为:[$\frac{3}{4}$,2].
点评 本题考查了直线过定点问题、斜率计算公式及其应用,考查了推理能力与计算能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
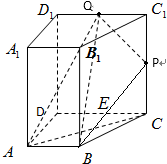 四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:
四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com