
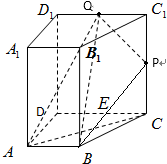
 四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:
四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:分析 (1)由已知结合三角形中位线定理证明四边形ABC1Q为平行四边形,从而得到AQ∥BC1,再由线面平行的判断得答案;
(2)取CD中点H,连接A1C1,B1Q,交于E,连接AC,BH交于F,可得四边形BHQB1为平行四边形,连接EF,BQ交于G,连接PG,则PG∥FC,再由线面平行的判定证明AC∥平面BPQ.
解答 证明:(1)如图,连接BC1,∵AB∥CD,CD∥C1Q,∴AB∥C1Q,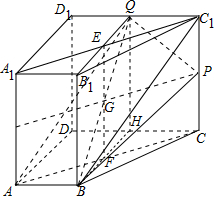
又AB=1,C1D1=2,Q为C1D1的中点,∴AB=C1Q,
则四边形ABC1Q为平行四边形,∴AQ∥BC1,
∵AQ?平面BCC1B1,BC1?平面BCC1B1,
∴AQ∥平面BCC1B1;
(2)取CD中点H,连接A1C1,B1Q,交于E,连接AC,BH交于F,
四边形BHQB1为平行四边形,连接EF,BQ交于G,连接PG,则PG∥FC,
即AC∥PG,
∵PG?平面PBQ,AC?平面PBQ,
∴AC∥平面BPQ.
点评 本题考查线面平行的判定,证明直线和平面的平行问题,常借助于三角形的中位线证得线线平行,是中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-15,1] | B. | (-∞,0] | C. | (-∞,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com